第二章 通信信道

2.1 通信信道的定义及分类

  • 信道：指以传输媒介为基础的信号通路 作用是传输信号

    • 狭义信道：有线信道、无线信道
    • 广义信道：调制信道（模拟通信系统）、编码信道（数字通信系统）

2.2 通信信道模型

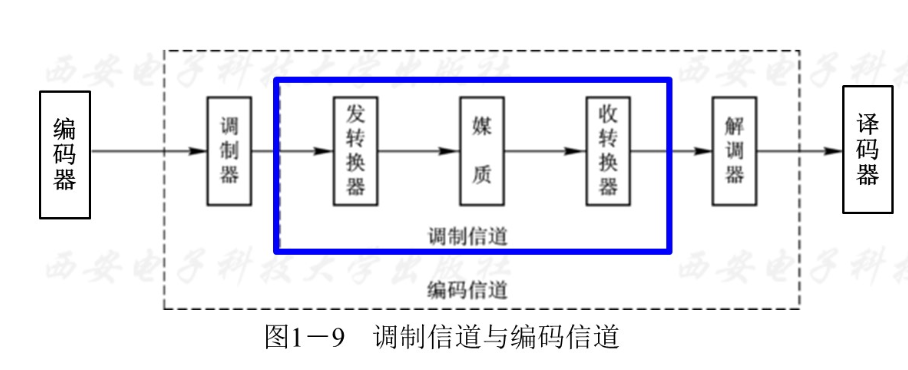
（1）调制信道：

从调制器的输出端到解调器的输入端

image-20250305104747112.png

主要特性：

  • ①有一对或多对输入端，则必有一对或多对输出端
  • ②绝大部分信道是线性的，即满足叠加原理
  • ③信号通过信道需要一定的迟延
  • ④信道对信号有损耗（固定损耗或时变损耗）
  • ⑤即使没有信号输入，在信道的输出端仍可能存在一定的功率输出（噪声）

可使用二对端（或多对端）的时变线性网络替代：

image-20250305105155757.png

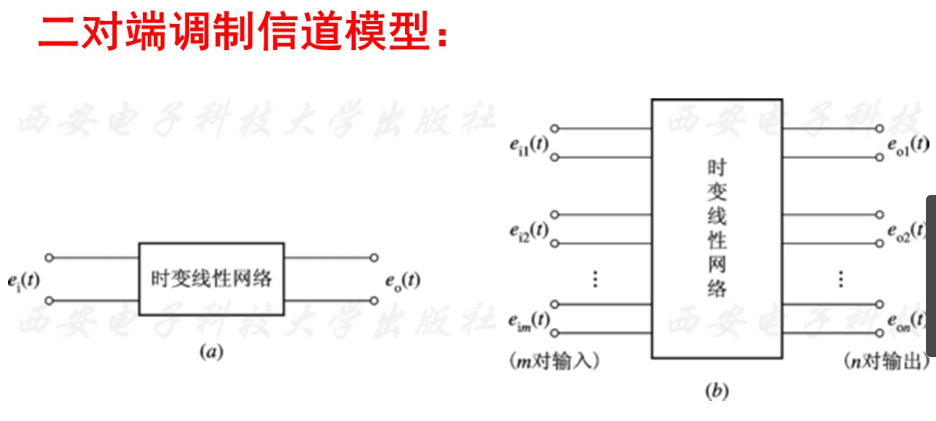
输入输出关系式： $e_{o}(t) = f[e_{i}(t)]+n(t)$

  • 其中 $e_{o}(t)$ 为信道输出信号 $e_{i}(t)$ 为信道输入信号 $n(t)$ 为信道噪声

  • 其其中 $f[e_{i}(t)]$ 为信道对信号影响的某种函数关系，也可以写成乘性干扰+加性干扰的形式：$f[e_i(t)] = k(t) \cdot e_{i}(t)+n(t)$

    • 加性干扰$n(t)$：人为造成或者外界环境噪声
    • 乘性干扰$k(t)$：复杂函数（线性畸变、非线性失真、时间延迟及衰减等）或随时间变化的特性

调制信道的分类：

  • 恒参信道：$k(t)不随时间t变化或变化极其缓慢$
  • 随参信道：$k(t)随时间t随机变化$
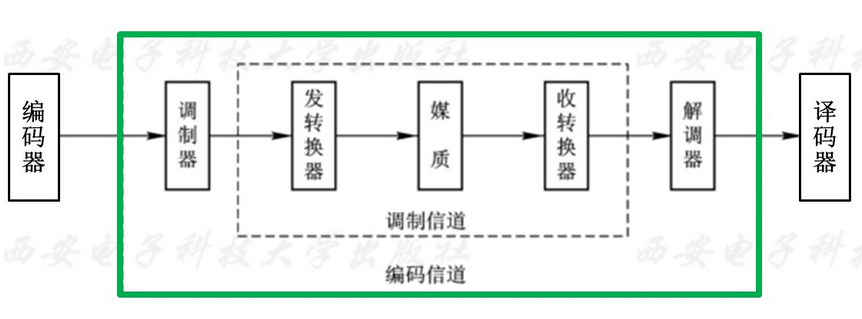
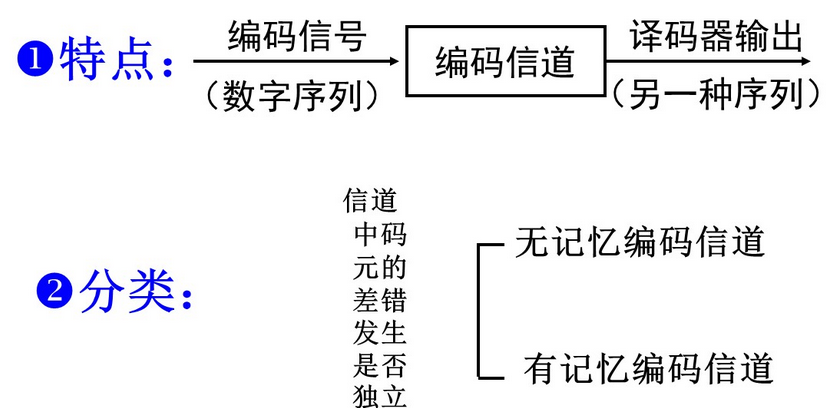
（2）编码信道：

从编码器的输出端到译码器的输入端

image-20250305110526874.png

image-20250305110614753.png

主要特点：

  • ①包括调制器、解调器、发送变换器以及传输媒介
  • ②对信号的影响是数字序列的变换
  • ③调制信道不理想会导致编码信道产生错码，且调制信道越差发生错误的概率越大
  • ④有时候编码信道可以看成一种数字信道

编码信道的模型可用数字信号信道转移概率来描述

①二进制无记忆编码信道模型

image-20250305111008108.png

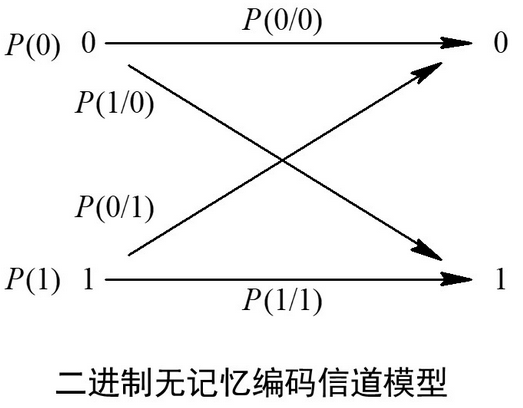
  • 正确转移概率：$P(0/0)和P(1/1)$
  • 错误转移概率：$P(0/1)和P(1/0)$
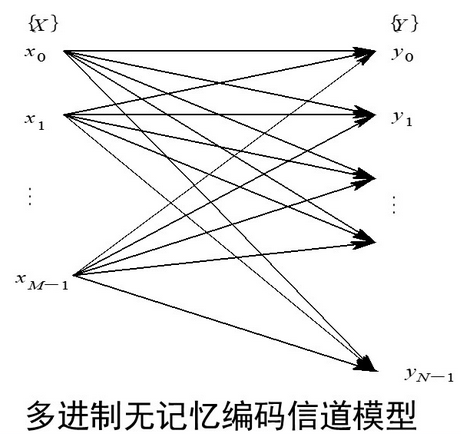
②多进制无记忆编码信道模型

image-20250305111204254.png

（3）信道带宽：

信号带宽表达式：$B = f_2 - f_1$ 单位$Hz$

  • 其中，$f_1$是信道能通过的最低频率，$f_2$是信道能通过的最高频率

2.3 信道噪声和干扰

  • 通常将加性噪声$n(t)$分为自然噪声和人为干扰，它们降低了接收信号的信干比，从而影响接收机的正常工作，导致模拟通信产生失真，数字通信产生误码

噪声：

（1）标准Ⅰ：高斯噪声

指概率密度函数服从高斯分布（即正态分布）

高斯噪声的一维概率密度函数表示：$p(x) = \frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(x-a)^2}{2\sigma^2}]$

image-20250305112516214.png

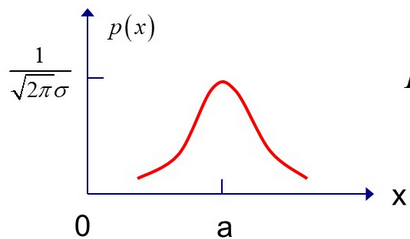
当噪声均值a=0为零时，噪声的平均功率等于噪声的方差，即：$P_n = \sigma^2$

（2）标准Ⅱ：白噪声

指功率谱密度函数在整个频域范围内是常数，即功率谱密度函数在频域内均匀分布：

image-20250305112834118.png

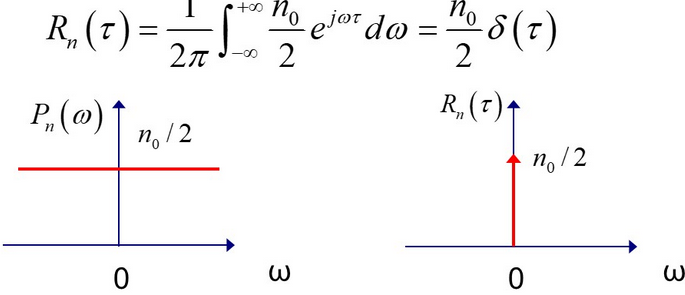
不符合上述条件的噪声称为有色噪声

（3）高斯白噪声

指噪声的概率密度函数满足正态分布统计特性，其功率谱密度函数是常数

  • 典型的高斯白噪声：热噪声

!!!在通信系统的理论分析中，特别是在分析、计算系统抗噪声性能时，经常假定系统中信道噪声为高斯型白噪声 WHY？？

  • 1.高斯型白噪声确实反映了实际信道中的加性噪声情况，比较真实地代表了信道噪声的特性
  • 2.高斯型白噪声可用具体的数学表达式表述，便于推导分析和运算

干扰：

image-20250305113500201.png

2.4 信道容量

信道容量：用于衡量物理信道能够传输数据的最大能力的基本标准，常以单位时间内信道中信息能够无差错传输的最大平均信息速率表征

有时也表示为单位时间内可传输的二进制位的位数，即信道的数据传输速率（位速率），单位为：位/秒(b/s) 简记为bps

分类：连续信道（模拟通信系统）、离散信道（数字通信系统）

（1）香农公式

无差错传输的最大信息速率C(信道容量)为：

$C=Blog_2(1+\frac{S}{n_0{B}}) (b/s)$

其中噪声功率$N=n_0{B}$，因此也可化为信噪比式子$S/N = S/n_0{B}$

结论：

  • 任何一个连续信道都有信道容量。实际传输速率（一般地）要求不能大于信道容量，除非允许存在一定的差错率
  • 增大信号功率 $S$ 可以增加信道容量 $C$
  • 当信道容量保持不变时，信道带宽 $B$ 、信号噪声功率比 $S/N$ 及传输时间三者是可以互换的
（2）离散信道容量

广义信道中的编码信道就是一种离散信道，常用转移概率描述

  • $P(x_i)$ 信源发送符号$x_i$的概率
  • $P(y_j)$ 接收端收到$y_j$的海女
  • $P(x_i|y_j)$ 在发送$x_i$的条件下收到$y_j$的条件概率，也称转移概率
①平均信息熵

$H(x)= -\sum^n_{i=1}P(x_i)log_2P(x_i) (b/s)$

②因信道噪声而损失的平均信息量

$H(x|y) = -\sum^m_{j=1}P(y_i)\sum^n_{i=1}P(x_i|y_i)log_2P(x_i|y)i$

③信道每秒传输的平均信息量

信息传输速率R

$R = r[H(x)-H(x|y)]$

符号速率r，指信道每秒传输的符号数

④信道容量

对一切可能的信源概率分布，求信息传输速率R的最大值即可：

$C = \max_{P(x)}\{r[H(x)-H(x|y)]\} (b/s)$