前言

本篇内容来自河南大学《数字通信原理》课程PPT，习题来自《数字通信原理》（第二版）课后习题，格式由DeepSeek R1润色。

第一章数字通信原理的基本概念

1.1 数字通信发展简史

1.2 数字通信的基本概念

1. 通信的定义

广义定义：通信是指需要信息的双方或多方在不违背各自意愿的情况下，采用任意方法、任意媒介，将信息从某一方准确、安全地送到另一方。
狭义定义：通信是信息的传输与交换，即信息的传递。

2. 通信的分类

按传输媒介：有线通信、无线通信
按信道中所传信号：模拟通信、数字通信
按工作频段：低频通信、高频通信等
按调制方式：基带传输、频带传输

3. 通信方式的分类

按信息传送方向与时间：单工通信、半双工通信、双工通信
按数字信号顺序：串行传输、并行传输
按通信网络形式：点到点通信、点到多点通信、多点到多点通信

4. 通信系统按所传信息的信号表现形式

模拟通信系统
数字通信系统

1.3 数字通信系统的基本组成

通信系统：传输信息所需技术设备的总和。

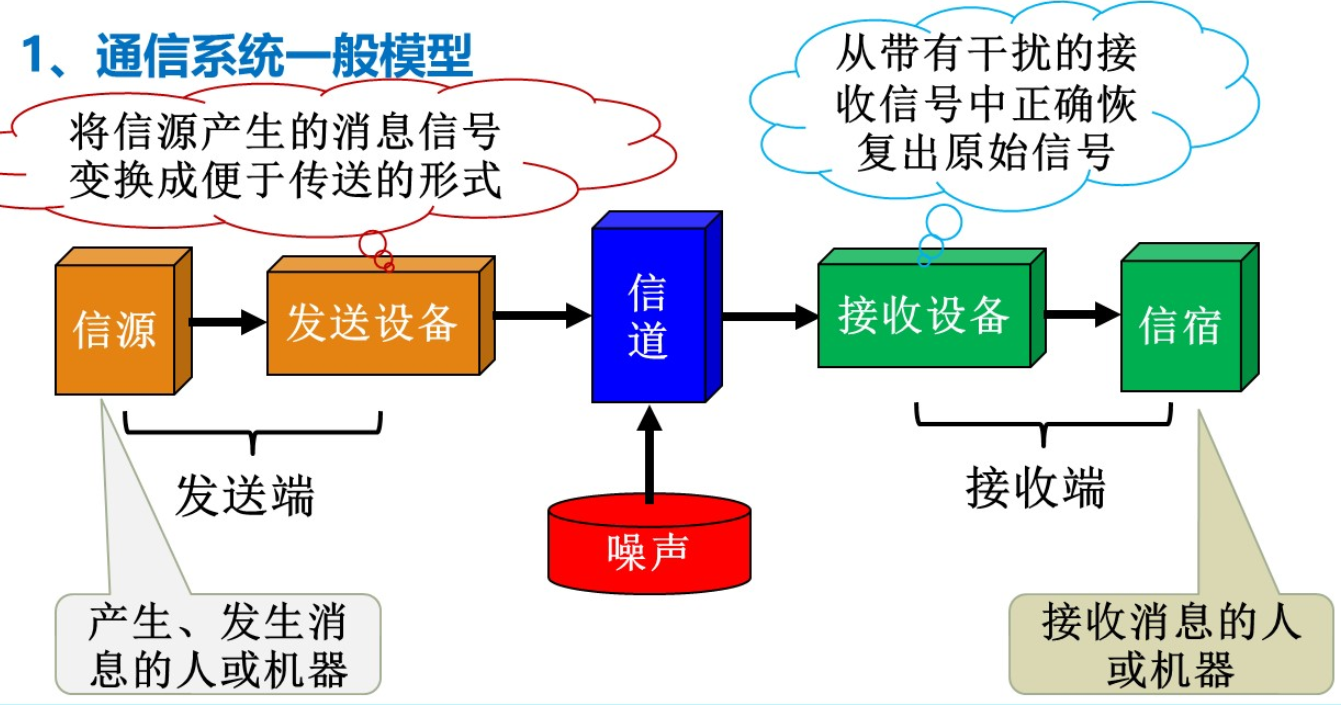
通信系统的一般模型（从左到右）：
- 发送端：信源 → 发送设备
- 信道（噪声影响）
- 接收端：接收设备 → 信宿
信源信号分类：
- 模拟信号（连续信号）
- 数字信号（离散信号）
噪声：通信系统中不希望出现的干扰信号，可分为：
- 内部干扰
- 外部干扰（多由信道引入）

1.4 数字通信系统框图

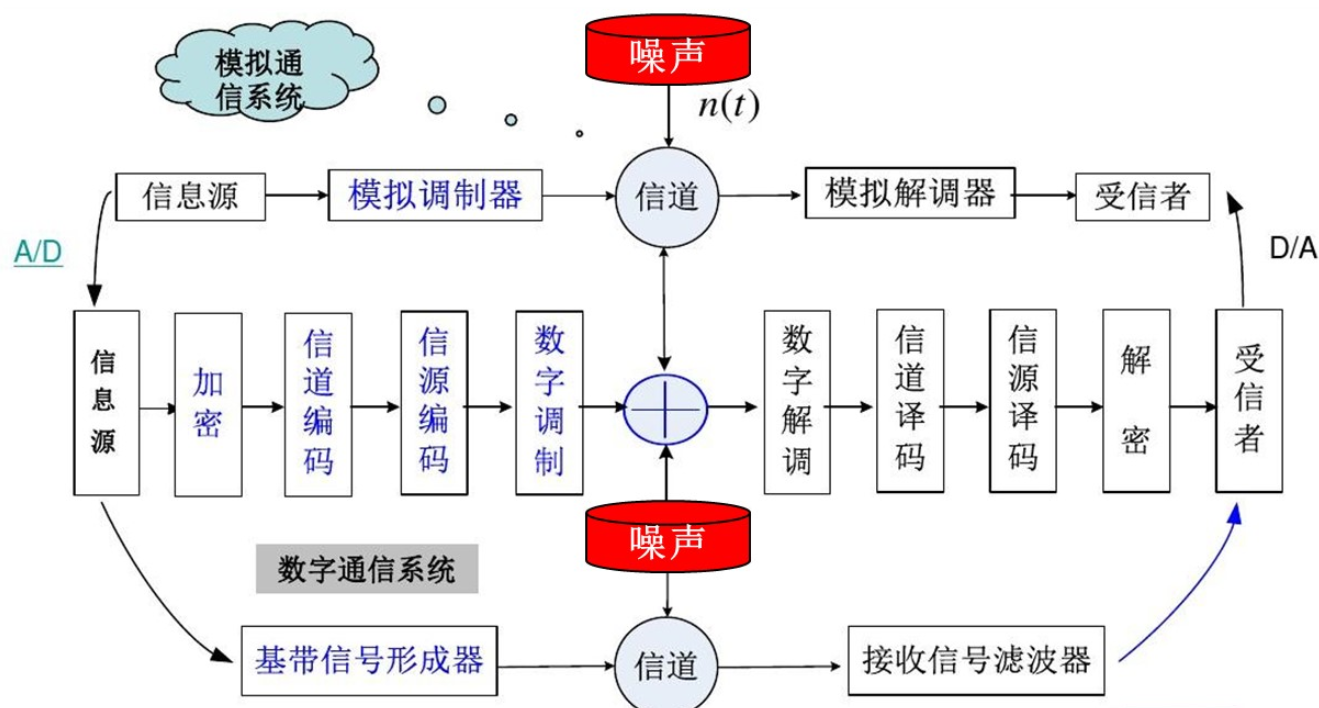
信源编码：提高信息传输的有效性。
信道编码：提高信息传输的可靠性。
调制：
- 用基带信号对载波信号的特定参数进行控制，实现信息的寄载。
- 将基带信号的频谱搬移到适合信道传输的频段。
加密与解密：保证信息传输的安全性。
同步：确保收发双方的节拍一致，避免因步调不一致而导致混乱。
复接与分接：
- 复接：将多路低速信号合成为一路高速信号，便于统一传输。
- 分接：复接的逆过程。

1.5 数字通信系统的优缺点

优点

抗噪声性能好
差错可控
保密性好
便于处理、变换和存储
易于集成，方便小型化

缺点

频带利用率不高
需要严格的同步系统

1.6 信息及其度量

信息的基本概念

信息：信息的内涵
消息：信息的载体
信号：消息的物理表现形式（模拟信号、数字信号）

信息的度量

信息量 $I$
- 衡量传输信息的多少。
- 数学表达式：
  $$I = -\log_a P(x) = \log_a \frac{1}{P(x)}$$
- 性质：
  - 消息出现的概率越小，信息量越大；反之，信息量越小。
  - 若干个互相独立事件的信息量等于各独立事件信息量之和：
    $$I[P_1(x) \cdot P_2(x) \cdot \cdots] = I[P_1(x)] + I[P_2(x)] + \cdots$$
- 单位：
  - $a=2$ 时，单位为比特（bit）
  - $a=e$ 时，单位为奈特（nat）
  - $a=10$ 时，单位为笛特（Det）
平均信息量 $\bar{I}$
- 又称信息熵，记为 $H(x)$，单位为 $bit/符号$。
- 数学表达式：
  $$H(x) = -\sum_{i=1}^N P(x_i) \log_2 P(x_i)$$
- 性质：
  - 信息源中各种符号等概率出现时，信息熵 $H$ 最大。

1.7 数字通信系统的性能指标

涉及要素

有效性：反映通信系统的传输容量。
可靠性：反映通信系统的传输质量。
安全性
适应性
经济性
标准性
维修性
工艺性

注：通信系统的有效性和可靠性通常是相互矛盾的。

1. 有效性指标

传输速率
- 码源传输速率 $R_B$
  - 单位时间内传输的码元数目（波特率），单位为波特 $B$。
  - 公式：
    $$R_B = \frac{1}{T_b}$$
- 信息传输速率 $R_b$
  - 单位时间内传输的信息量，单位为比特/秒（$bit/s$）。
- 二者关系：
  $$R_b = R_B \cdot \log_2 N$$
频带利用率 $\eta$
- 定义：单位频带内传输速率的大小。
  $$\eta = \frac{R_B}{B} \, (\text{B/Hz})$$
  $$\eta = \frac{R_b}{B} \, (\text{bit/s/Hz})$$

2. 可靠性指标

信噪比 ($S/N$)
- 定义：信号功率 $S$ 与噪声功率 $N$ 的比值。
  $$SNR = \frac{S}{N} \quad \text{或} \quad (SNR)_{dB} = 10 \log_{10} \frac{S}{N}$$
误码率 $P_e$
- 定义：接收错误的码元数在传输的总码元数中所占的比例。
  $$P_e = \lim_{N \to \infty} \frac{\text{错误码元数 } n}{\text{传输总码元数 } N}$$
误信率 $P_{eb}$
- 定义：接收错误的信息量在传输总信息量中所占的比例。
  $$P_{eb} = \lim_{N_b \to \infty} \frac{\text{错误比特数 } n_b}{\text{传输总比特数 } N_b}$$
$P_e$ 与 $P_{eb}$ 的关系
- 二进制：$P_e = P_{eb}$
- M 进制：$P_{eb} \approx \frac{1}{2} P_e$

1.8 第一章习题

数字通信的特点有哪些？

优点：

抗噪声性能好
差错可控
保密性好
便于处理、变换和存储
易于集成，方便小型化

缺点：

频带利用率不高
需要严格的同步系统

设英文字母 E 出现的概率为 0.105，x 出现的概率为 0.002。试求 E 和 x 的信息量。

$$I_{E} = \log_{2}\frac{1}{P(E)} = \log_{2}\frac{1}{0.105} = 3.25 \, \text{bit}$$
$$I_{x} = \log_{2}\frac{1}{P(x)} = \log_{2}\frac{1}{0.002} = 8.97 \, \text{bit}$$

信息源的符号集由 A、B、C、D 和 E 组成，设每一符号独立出现，其出现的概率为 3/16、1/8、1/8、1/4 和 5/16。试求该信息源符号的平均信息量。

$$H(x) = -\sum_{i=1}^{N}P(x_{i})\log_{2}P(x_{i})$$

$$= -\frac{3}{16}\log_{2}\frac{3}{16} - \frac{1}{8}\log_{2}\frac{1}{8} - \frac{1}{8}\log_{2}\frac{1}{8} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{5}{16}\log_{2}\frac{5}{16}$$

$$= 0.45 + 0.375 + 0.375 + 0.5 + 0.52 = 2.22 \, (\text{bit/符号})$$

一个由字母 A、B、C、D 组成的字。对于传输的每一个字母用二进制脉冲编码，00 代替 A，01 代替 B，10 代替 C，11 代替 D。每个脉冲宽度为 5ms。
（1）不同的字母是等概率出现时，试计算传输的平均信息速率。
（2）若每个字母出现的概率为 $P_A = 1/5$，$P_B = 1/4$，$P_C = 1/4$，$P_D = 3/10$，试计算传输的平均信息速率。

(1)
$$H(x) = 4 \cdot -\frac{1}{4}\log_{2}\frac{1}{4} = 2 \, \text{bit/符号}$$

由于使用二进制脉冲编码，每个符号由两位二进制码构成，所以每个字母的持续时间为：
$$5 \, \text{ms} \cdot 2 = 10 \, \text{ms}$$

字母波特率：
$$R_{B} = \frac{1}{10 \, \text{ms}} = 100 \, \text{B}$$

平均信息速率：
$$R_{b} = R_{B} \cdot H(x) = 200 \, \text{bit/s}$$

(2)
$$H(x) = -\frac{1}{5}\log_{2}\frac{1}{5} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{3}{10}\log_{2}\frac{3}{10} = 1.985 \, \text{bit/符号}$$

平均信息速率：
$$R_{b} = R_{B} \cdot H(x) = 198.5 \, \text{bit/s}$$

国际莫尔斯电码用点和划的序列发送英文字母，划用持续 3 单位的电流脉冲表示，点用持续 1 单位的电流脉冲表示，且划出现的概率是点出现的概率的 1/3：
（1）计算点和划的信息量；
（2）计算点和划的平均信息量。

(1)
$P(dot)+P(line) = 1$ & $P(line) = \frac{1}{3} \cdot P(dot)$
->
$P(dot) = \frac{3}{4}$ & $P(line) = \frac{1}{4}$

信息量：
$$I_{\text{dot}} = -\log_{2}P(\text{dot}) = -\log_{2}\frac{3}{4} = 0.415 \, \text{bit}$$
$$I_{\text{line}} = -\log_{2}P(\text{line}) = 2 \, \text{bit}$$

(2)
平均信息量：
$$H(x) = -\sum P(x_{i})\log_{2}P(x_i) = 0.811 \, \text{bit/符号}$$