前言

本篇笔记整合自河南大学与哈尔滨工业大学《计算机组成原理》课程内容，经Deepseek-R1进行标准化格式优化。

第一章 计算机系统概论

1.1 计算机系统简介

一、计算机的软硬件概念

1. 计算机系统

计算机系统分为硬件和软件：

• 硬件：计算机系统的实体（如主机、外设等）

• 软件：由功能程序构成，分为：

  • 系统软件：管理计算机系统（操作系统、语言处理程序、数据库管理系统等）
  • 应用软件：任务专用程序（如办公软件、图像处理工具）

二、计算机系统的层次结构

1. 抽象方法论

系统复杂性管理的核心方法是抽象，可分为：

• 物理层抽象
• 程序员视角抽象

2. 五层结构体系

3. 体系结构与组成

• 计算机体系结构：程序员可见的系统属性（指令集、内存模型）
• 计算机组成：体系结构的具体实现（数据通路设计、控制单元实现）

1.2 计算机的基本组成

一、冯·诺依曼体系特征

1.五大组成部分：输入设备、存储器、运算器、控制器、输出设备

2.指令和数据以同等地位存于存储器，可按地址寻访

3.指令和数据都用二进制表示

4.指令由操作码和地址码组成

5.存储程序

6.以运算器为中心

二、计算机硬件框图

1.以存储器为中心的计算机硬件框图

2.现代计算机硬件框图

• 系统复杂性管理方法：

  ①层次化；②模块化；③规则性

3.主机的构成

（1）存储器的基本组成

存储体——存储单元——存储元件

• 存储单元存放一串二进制代码
• 存储字存储单元中二进制代码的组合
• 存储字长存储单元中二进制代码的位数
• 在存储器中按地址寻访

基本组成：

• MAR：存储器地址寄存器 反映存储单元的个数
• MDR：存储器数据存储器 反映存储字长

（2）运算器的基本组成及操作过程

基本组成：

• ACC：累加器
• MQ：乘商寄存器
• ALU：算数逻辑单元
• X：数据寄存器

（3）控制器的基本组成和功能

功能：解释指令；保证指令按序执行

基本组成：

• PC：程序寄存器
• IR：指令寄存器
• CU：控制单元

（4）主机完成一条指令的过程

以取数指令为例：

以存数指令为例：

1.3 计算机硬件技术指标

核心指标体系

*性能优化公式

吉普森法综合评估：

​ 也用来作为计算机运算速度的技术指标评估

$$ T_M = \sum_{i=1}^{n} f_i t_i $$

• $f_i$：第i类操作频度
• $t_i$：第i类操作耗时

前言

本篇内容来自河南大学《数字通信原理》课程PPT，习题来自《数字通信原理》（第二版）课后习题，格式由DeepSeek R1润色。

第一章 数字通信原理的基本概念

1.1 数字通信发展简史

1.2 数字通信的基本概念

1. 通信的定义

• 广义定义：通信是指需要信息的双方或多方在不违背各自意愿的情况下，采用任意方法、任意媒介，将信息从某一方准确、安全地送到另一方。
• 狭义定义：通信是信息的传输与交换，即信息的传递。

2. 通信的分类

• 按传输媒介：有线通信、无线通信
• 按信道中所传信号：模拟通信、数字通信
• 按工作频段：低频通信、高频通信等
• 按调制方式：基带传输、频带传输

3. 通信方式的分类

• 按信息传送方向与时间：单工通信、半双工通信、双工通信
• 按数字信号顺序：串行传输、并行传输
• 按通信网络形式：点到点通信、点到多点通信、多点到多点通信

4. 通信系统按所传信息的信号表现形式

• 模拟通信系统
• 数字通信系统

1.3 数字通信系统的基本组成

通信系统：传输信息所需技术设备的总和。

1. 通信系统的一般模型（从左到右）：

   • 发送端：信源 → 发送设备
   • 信道（噪声影响）
   • 接收端：接收设备 → 信宿

2. 信源信号分类：

   • 模拟信号（连续信号）
   • 数字信号（离散信号）

3. 噪声：通信系统中不希望出现的干扰信号，可分为：

   • 内部干扰
   • 外部干扰（多由信道引入）

1.4 数字通信系统框图

1. 信源编码：提高信息传输的有效性。
2. 信道编码：提高信息传输的可靠性。

3. 调制：

   • 用基带信号对载波信号的特定参数进行控制，实现信息的寄载。
   • 将基带信号的频谱搬移到适合信道传输的频段。
4. 加密与解密：保证信息传输的安全性。
5. 同步：确保收发双方的节拍一致，避免因步调不一致而导致混乱。

6. 复接与分接：

   • 复接：将多路低速信号合成为一路高速信号，便于统一传输。
   • 分接：复接的逆过程。

1.5 数字通信系统的优缺点

优点

1. 抗噪声性能好
2. 差错可控
3. 保密性好
4. 便于处理、变换和存储
5. 易于集成，方便小型化

缺点

1. 频带利用率不高
2. 需要严格的同步系统

1.6 信息及其度量

信息的基本概念

• 信息：信息的内涵
• 消息：信息的载体
• 信号：消息的物理表现形式（模拟信号、数字信号）

信息的度量

1. 信息量 $I$

   • 衡量传输信息的多少。
   • 数学表达式：
     $$I = -\log_a P(x) = \log_a \frac{1}{P(x)}$$

   • 性质：

     • 消息出现的概率越小，信息量越大；反之，信息量越小。
     • 若干个互相独立事件的信息量等于各独立事件信息量之和：
       $$I[P_1(x) \cdot P_2(x) \cdot \cdots] = I[P_1(x)] + I[P_2(x)] + \cdots$$

   • 单位：

     • $a=2$ 时，单位为比特（bit）
     • $a=e$ 时，单位为奈特（nat）
     • $a=10$ 时，单位为笛特（Det）

2. 平均信息量 $\bar{I}$

   • 又称信息熵，记为 $H(x)$，单位为 $bit/符号$。
   • 数学表达式：
     $$H(x) = -\sum_{i=1}^N P(x_i) \log_2 P(x_i)$$

   • 性质：

     • 信息源中各种符号等概率出现时，信息熵 $H$ 最大。

1.7 数字通信系统的性能指标

涉及要素

• 有效性：反映通信系统的传输容量。
• 可靠性：反映通信系统的传输质量。
• 安全性
• 适应性
• 经济性
• 标准性
• 维修性
• 工艺性

注：通信系统的有效性和可靠性通常是相互矛盾的。

1. 有效性指标

1. 传输速率

   • 码源传输速率 $R_B$

     • 单位时间内传输的码元数目（波特率），单位为波特 $B$。
     • 公式：
       $$R_B = \frac{1}{T_b}$$

   • 信息传输速率 $R_b$

     • 单位时间内传输的信息量，单位为比特/秒（$bit/s$）。
   • 二者关系：
     $$R_b = R_B \cdot \log_2 N$$

2. 频带利用率 $\eta$

   • 定义：单位频带内传输速率的大小。
     $$\eta = \frac{R_B}{B} \, (\text{B/Hz})$$
     $$\eta = \frac{R_b}{B} \, (\text{bit/s/Hz})$$

2. 可靠性指标

1. 信噪比 ($S/N$)

   • 定义：信号功率 $S$ 与噪声功率 $N$ 的比值。
     $$SNR = \frac{S}{N} \quad \text{或} \quad (SNR)_{dB} = 10 \log_{10} \frac{S}{N}$$

2. 误码率 $P_e$

   • 定义：接收错误的码元数在传输的总码元数中所占的比例。
     $$P_e = \lim_{N \to \infty} \frac{\text{错误码元数 } n}{\text{传输总码元数 } N}$$

3. 误信率 $P_{eb}$

   • 定义：接收错误的信息量在传输总信息量中所占的比例。
     $$P_{eb} = \lim_{N_b \to \infty} \frac{\text{错误比特数 } n_b}{\text{传输总比特数 } N_b}$$

4. $P_e$ 与 $P_{eb}$ 的关系

   • 二进制：$P_e = P_{eb}$
   • M 进制：$P_{eb} \approx \frac{1}{2} P_e$

1.8 第一章习题

3. 数字通信的特点有哪些？

优点：

1. 抗噪声性能好
2. 差错可控
3. 保密性好
4. 便于处理、变换和存储
5. 易于集成，方便小型化

缺点：

1. 频带利用率不高
2. 需要严格的同步系统

5. 设英文字母 E 出现的概率为 0.105，x 出现的概率为 0.002。试求 E 和 x 的信息量。

$$I_{E} = \log_{2}\frac{1}{P(E)} = \log_{2}\frac{1}{0.105} = 3.25 \, \text{bit}$$
$$I_{x} = \log_{2}\frac{1}{P(x)} = \log_{2}\frac{1}{0.002} = 8.97 \, \text{bit}$$

6. 信息源的符号集由 A、B、C、D 和 E 组成，设每一符号独立出现，其出现的概率为 3/16、1/8、1/8、1/4 和 5/16。试求该信息源符号的平均信息量。

$$H(x) = -\sum_{i=1}^{N}P(x_{i})\log_{2}P(x_{i})$$

$$= -\frac{3}{16}\log_{2}\frac{3}{16} - \frac{1}{8}\log_{2}\frac{1}{8} - \frac{1}{8}\log_{2}\frac{1}{8} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{5}{16}\log_{2}\frac{5}{16}$$

$$= 0.45 + 0.375 + 0.375 + 0.5 + 0.52 = 2.22 \, (\text{bit/符号})$$

8. 一个由字母 A、B、C、D 组成的字。对于传输的每一个字母用二进制脉冲编码，00 代替 A，01 代替 B，10 代替 C，11 代替 D。每个脉冲宽度为 5ms。

   （1）不同的字母是等概率出现时，试计算传输的平均信息速率。
   （2）若每个字母出现的概率为 $P_A = 1/5$，$P_B = 1/4$，$P_C = 1/4$，$P_D = 3/10$，试计算传输的平均信息速率。

(1)
$$H(x) = 4 \cdot -\frac{1}{4}\log_{2}\frac{1}{4} = 2 \, \text{bit/符号}$$

由于使用二进制脉冲编码，每个符号由两位二进制码构成，所以每个字母的持续时间为：
$$5 \, \text{ms} \cdot 2 = 10 \, \text{ms}$$

字母波特率：
$$R_{B} = \frac{1}{10 \, \text{ms}} = 100 \, \text{B}$$

平均信息速率：
$$R_{b} = R_{B} \cdot H(x) = 200 \, \text{bit/s}$$

(2)
$$H(x) = -\frac{1}{5}\log_{2}\frac{1}{5} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{1}{4}\log_{2}\frac{1}{4} - \frac{3}{10}\log_{2}\frac{3}{10} = 1.985 \, \text{bit/符号}$$

平均信息速率：
$$R_{b} = R_{B} \cdot H(x) = 198.5 \, \text{bit/s}$$

9. 国际莫尔斯电码用点和划的序列发送英文字母，划用持续 3 单位的电流脉冲表示，点用持续 1 单位的电流脉冲表示，且划出现的概率是点出现的概率的 1/3：

   （1）计算点和划的信息量；
   （2）计算点和划的平均信息量。

(1)
$P(dot)+P(line) = 1$ & $P(line) = \frac{1}{3} \cdot P(dot)$
->
$P(dot) = \frac{3}{4}$ & $P(line) = \frac{1}{4}$

信息量：
$$I_{\text{dot}} = -\log_{2}P(\text{dot}) = -\log_{2}\frac{3}{4} = 0.415 \, \text{bit}$$
$$I_{\text{line}} = -\log_{2}P(\text{line}) = 2 \, \text{bit}$$

(2)
平均信息量：
$$H(x) = -\sum P(x_{i})\log_{2}P(x_i) = 0.811 \, \text{bit/符号}$$

11. 对于二电平数字信号，每秒钟传输 300 个码元，问：此传码率等于多少？若数字信号 0 和 1 出现是独立等概率的，那么传信率等于多少？

传码率：
$$R_{B} = 300 \, \text{B}$$

传信率：
由于题中为二电平数字信号且 0 和 1 出现独立等概率，则：
$$R_{b} = R_{B} \cdot \log_{2}2 = 300 \, \text{bit/s}$$

14. 设数字信号码元时间长度为 $1 \, \mu s$，如采用四电平传输，求信息传输速率及符号速率，若传输过程中 2s 错误 1 个 bit，求误码率。

传码率：
$$R_{B4} = \frac{1}{1 \, \mu s} = 10^{6} \, \text{B}$$

传信率：
$$R_{b4} = R_{B4} \cdot \log_{2}4 = 2 \cdot 10^{6} \, \text{bit/s}$$

误码率：
$$P_{e} = \frac{1}{2 \cdot 10^{6} \cdot 2} = 2.5 \cdot 10^{-7}$$

15. 假设数字通信系统的频带宽度为 1024kHz，可传输 2048kbit/s 的比特率，问：其频带利用率为多少 bit/s/Hz？

$$\eta = \frac{\text{信息传输速率}}{\text{频带带宽}} = \frac{R_{b}}{B} = \frac{2048 \, \text{kbit/s}}{1024 \, \text{kHz}} = 2 \, (\text{bit/s/Hz})$$

前言

笔记部分基于王道考研系列课程，习题部分来自谢希仁第八版《计算机网络》，格式方面由OpenAI ChatGPT-4o优化完善。

第一章 计算机网络体系结构

1.1 计算机网络概述

1.1.1 计算机网络的概念

1. 计算机网络（简称网络）由若干结点（node）和连接结点的链路（link）组成。
2. 通过路由器（router）互连构成的覆盖范围更广的计算机网络，称作互连网（internet）。
3. 当前全球最大的、开放的、由众多网络和路由器互连形成的计算机网络，通常用专有名词互联网（Internet）表示。
4. 互连网（internet）内部不一定使用 TCP/IP 协议，而互联网（Internet）为了统一，一般使用 TCP/IP 协议族作为通信规则。

1.1.2 计算机网络的组成和功能

1. 计算机网络的组成：

从组成成分看

从工作方式看

从逻辑功能看

2. 计算机网络的功能：数据通信（最基本、最重要）、资源共享、分布式处理、提高可靠性、负载均衡、其它。

1.1.3 电路交换、报文交换、分组交换

电路交换

通过物理线路连接，动态地分配传输线路资源。

电路交换的过程：建立连接 $\rightarrow$ 通信 $\rightarrow$ 释放连接。

优点：建立一条专用物理通路，用户双方独占线路资源，数据传输速率高。

缺点：

1. 建立/释放连接需要额外的时间开销；
2. 线路被通信双方独占，利用率低；
3. 线路分配的灵活性差；
4. 交换结点不支持“差错控制”。

因此，电路交换更适用于：低频次、大量地传输数据。

报文（Message）交换

由控制信息和用户数据组成。

优点：

1. 通信前无需建立连接；
2. 数据以“报文”为单位被交换结点间“存储转发”，通信线路可以灵活分配；
3. 通信时间内，两个用户无需独占一整条物理线路，相比于电路交换，线路利用率高；
4. 交换节点支持“差错控制”。

缺点：

1. 报文不定长，不方便存储转发管理；
2. 长报文的存储转发时间开销大、缓存开销大；
3. 长报文容易出错，重传代价高。

分组交换（基于报文交换）

由报文拆分成定长的分组（Packet），每一个分组由首部（Header）和数据组成，其中首部即分组的控制信息，由源地址、目的地址、分组号等组成。

优点：继承报文交换的全部优点，但改善了不定长的问题：

1. 方便存储转发管理；
2. 分组存储转发时间开销小、缓存开销小；
3. 分组不易出错，重传代价低。

缺点：

1. 相比于报文交换，控制信息占比增加；
2. 相比于电路交换，依然存在存储转发时延；
3. 报文被拆分为多个分组，传输过程中可能出现失序、丢失或重复分组的问题。

虚电路交换技术（基于分组交换）

电路交换、报文交换、分组交换的性能分析：

1.1.4 计算机网络的分类

按分布范围分类

• 广域网（WAN）、城域网（MAN）、局域网（LAN）、个域网（PAN）。
• 城域网和局域网的通信技术：以太网技术。“以太网”现在几乎成为了“局域网”的代名词。
• 通常通过无线技术将个人设备连接起来的网络也称为无线个域网（WPAN）：网关 + 设备。

按传输技术分类

• 广播式网络、点对点网络。

按拓扑结构分类

逻辑上存在四类：

1. 总线形结构：数据“广播式”传输；存在“总线争用”的问题（集线器连接）。
2. 环形结构：数据“广播式”传播；通过“令牌”解决总线争用问题，令牌顺环形依次传递，持令牌者可使用总线（令牌环网）。
3. 星形结构：由中央设备实现数据的“点对点”传输；不存在总线争用问题（以太网交换机）。
4. 网状结构：由中间结点统一存储转发，属于“点对点”传输（广域网）。

按使用者分类

• 公用网、专用网。

按传输介质分类

• 有线网络、无线网络。

1.1.5 计算机网络的性能指标

PART I 速率、带宽、吞吐量

1. 信道：表示向某一方向传送信息的通道。

   • 信道 ≠ 通信线路。
   • 一条通信线路在逻辑上往往对应一条发送信道和一条接收信道。

2. 速率：连接到网络上的节点在信道上传输数据的速率，也称数据率或比特率、数据传输速率。

   • 速率单位：bit/s 或 b/s 或 bps，有时也用 B/s（1 Byte = 8 Bit）。
   • 常用数量前缀：$k(10^3)$, $M(10^6)$, $G(10^9)$, $T(10^{12})$。

   注意：在计组、操作系统中，数据前缀含义不同：
   $K(2^{10})$, $M(2^{20})$, $G(2^{30})$, $T(2^{40})$。

3. 带宽（bandwidth）：某信道所能传输的最高数据率。

   • 节点间通信实际能达到的最高速率由带宽和节点性能共同限制。
   • 常见带宽单位：bps。

   注意：在《通信原理》中，带宽表示某信道允许通过的信号频带范围，单位为 Hz（相关理论如香农定理、奈式准则）。

   

4. 吞吐量：单位时间内通过某个网络（或信道、接口）的实际数据量，受到带宽限制及复杂网络负载情况的影响。

PART II 时延、时延带宽积、往返时延

1. 时延（Delay）：指数据从网络的一端传送到另一端所需要的时间，有时也称为延迟或迟延。
   总时延 = 发送时延 + 传播时延 + 处理时延 + 排队时延

   • 发送时延（传输时延）：节点将数据推向信道所花费的时间：
     $$\text{发送时延} = \frac{\text{数据长度 (bit)}}{\text{发送速率 (bit/s)}}$$
   • 传播时延：电磁波在信道中传播一定距离所花费的时间：
     $$\text{传播时延} = \frac{\text{信道长度 (m)}}{\text{电磁波在信道中的传播速度 (m/s)}}$$
   • 处理时延：被路由器处理所花费的时间（一般不考虑）。
   • 排队时延：数据排队进入、排队发出路由器所花费的时间（一般不考虑）。
2. 时延带宽积（bit）：
   $$\text{时延带宽积} = \text{传播时延 (s)} \times \text{带宽 (bit/s)}$$
   含义：一条链路中，已经从发送端发出但尚未到达接收端的最大比特数（常用于设计最短帧长）。
3. 往返时延（RTT）：表示从发送方发送完数据，到发送方接收到来自接收方确认总共经历的时间。

PART III 信道利用率

信道利用率：某个信道有百分之多少的时间是有数据通过的。
$$\text{信道利用率} = \frac{\text{有数据通过的时间}}{\text{有数据通过的时间} + \text{没有数据通过的时间}}$$

1.2 计算机网络的分层结构

1.2.1 “分层”的设计思想

1. 类比“快递网络”的分层体系结构，将计算机网络分为五层：应用层、传输层、网络层、数据链路层、物理层；并将各种不同“功能”安排在合适的层次中。
2. 不同类型的节点实现的功能层次可能不一样（分层结构的设计并不唯一）。

1.2.2 三种计算机网络体系结构

1. OSI参考结构（法律上标准，由 ISO 组织提出）：

   • 应用层、表示层、会话层、运输层、网络层、数据链路层、物理层。

2. TCP/IP模型（事实上标准，ARPANET 项目成果）：

   • 应用层、运输层、网际层（也称 IP 层）、网络接口层。

3. 五层模型（教学用标准）：

   • 应用层、传输层、网络层、数据链路层、物理层。

   

网络体系结构的概念：是计算机网络的各层及其协议的集合，即构建计算机网络时需要完成的功能的精确定义（不涉及实现）。

1.2.3 计算机网络中各层之间的关系

水平视角

1. 实体：将第 n 层的活动元素（软件 + 硬件）称为第 n 层实体。
2. 不同机器上同一层称为对等层，同一层的实体称为对等实体。

3. 协议：即网络协议，是控制对等实体之间通信的规则集合，是水平的。主机或路由器中的协议层称为协议栈。

   

垂直视角

1. 接口：即同一节点内相邻两层的实体交换信息的逻辑接口，又称为服务访问点（SAP）。

2. 服务：指下层为紧邻的上层提供的功能调用，是垂直的。

   

1.2.4 PDU、SDU、PCI

1. 协议数据单元（PDU）：对等层次之间传送的数据单位，第 n 层的 PDU 记为 n-PDU。
2. 服务数据单元（SDU）：为完成上一层实体所要求的功能而传送的数据，第 n 层的 SDU 记为 n-SDU。
3. 协议控制信息（PCI）：控制协议操作的信息，第 n 层的 PCI 记为 n-PCI。

4. 三者间关系：
   $$n\text{-SDU} + n\text{-PCI} = n\text{-PDU} = (n-1)\text{-SDU}$$

   

1.2.5 协议

定义：即网络协议（Network protocol），是控制对等实体之间通信的规则集合，是水平的。
协议的三要素：语法、语义、同步。

1. 语法：数据与控制信息的格式。
2. 语义：即需要发出何种控制信息、完成何种动作以及做出何种应答。
3. 同步（或时序）：执行各种操作的条件、时序关系等，即事件实现顺序的详细说明。

1.2.6 两种参考模型

OSI 参考模型

1. 物理传输媒体（如网线）。
2. 物理层：实现相邻节点之间比特的传输。

3. 数据链路层

   ：确保相邻节点之间的链路逻辑上无差错。

   • 功能：差错控制、流量控制。

4. 网络层

   ：把“分组”从源节点转发到目的节点。

   • 功能：路由选择、分组转发、拥塞控制、网际互连等。

5. 传输层

   ：实现端到端通信，即实现进程到进程的通信（端指“端口”）。

   • 功能：复用和分用等。
6. 会话层：通过会话管理管理进程间会话。
7. 表示层：解决不同主机上信息表示不一致的问题。
8. 应用层：实现特定的网络应用。

各层数据传输单位：

• 应用层、表示层、会话层：报文（Message）。
• 传输层：报文段（Segment）。
• 网络层：分组（Packet）。
• 数据链路层：帧（Frame）。
• 物理层：比特（Bit）。

TCP/IP 模型

1. 物理传输媒体。
2. 网络接口层：实现相邻节点间的数据传输，但具体传输方式不做规定。

3. 网络层：

   • 功能：路由选择、分组转发、拥塞控制、网际互连。
   • 注意：差错控制、流量控制等功能交由传输层实现。
4. 传输层。
5. 应用层：实现特定的网络应用（按需）。

各层数据传输单位：

• 应用层：报文（Message）。
• 传输层：报文段（Segment）。
• 网络层：分组（Packet）。
• 网络接口层：帧（Frame）。

OSI 与 TCP/IP 模型对比

1.3 第一章习题

1-02 试简述分组交换的要点。

答：将报文拆分为若干分组(Packet)，每个分组定长且由首部(Header)与数据构成，其中首部包含控制信息如目的地址、源地址、分组号等。优点：高效灵活，分组转发时间、缓存开销小；不易出错、重传代价低。缺点：控制信息占比增加，存在额外开销；分组在路由器存储转发时需排队，存在时延。

1-03 试从多个方面比较电路交换，报文交换和分组交换的主要优缺点

答：

1) 电报交换：独占通信线路，可以连续传送大量数据的效率高；但也有通信线路利用率低、线路灵活性差、不支持差错控制的问题。

2) 报文交换：通信线路灵活性高，支持差错控制，相比电报交换线路利用率高；但由于报文不定长，不利于存储转发管理，并且长报文存在转发存储开销大、易出错、重传代价高的问题。

3) 分组交换：继承了报文交换的优点的同时通过分组改进了报文不定长的问题；但仍存在存储转发时延，并且控制信息比例相比报文交换增加，存在一定的额外开销。

1-10 试在下列条件下比较电路交换和分组交换。要传送的报文共 $x$（bit）。从源点到终点共经过 $k$ 段链路，每段链路的传播时延为 $d$（s），数据率为 $b$ (b/s)。在电路交换时电路的建立时间为 $s$ (s)。在分组交换时分组长度为 $p$ (bit)，且各结点的排队等待时间可忽略不计。问在怎样的条件下，分组交换的时延比电路交换的要小？（提示：画一下草图观察 $k$ 段链路共有几个结点。）

对于电路交换：

发送时延 $t_1 = \frac{x}{b}$，传播时延 $t_2 = k \cdot d$，电路建立时间 $t_3 = s$。

总时延 $T_{\text{电路}} = t_1 + t_2 + t_3 = \frac{x}{b} + k \cdot d + s$。

对于分组交换：

发送时延 $t_1 = \lceil \frac{x}{p} \rceil \cdot \frac{p}{b}$，传播时延 $t_2 = k \cdot d$，$k-1$ 个节点的发送时延 $t_3 = (k-1) \cdot \frac{p}{b}$。

总时延 $T_{\text{分组}} = t_1 + t_2 + t_3 = \lceil \frac{x}{p} \rceil \cdot \frac{p}{b} + k \cdot d + (k-1) \cdot \frac{p}{b}$。

则要使 $T_{\text{分组}} < T_{\text{电路}}$ 的条件为：$x \gg p$ 或 $x = k \cdot p$ 且 $k$ 为整数。

1-17 收发两端之间的传输距离为 $1000$ km，信号在媒体上的传播速率为 $2 \times 10^8$ m/s。试计算以下两种情况的发送时延和传播时延：
（1） 数据长度为 $10^7$ bit, 数据发送速率为 $100$ kb/s。
（2） 数据长度为 $10^3$ bit, 数据发送速率为 $1$ Gb/s。
从上面的计算中可以得到什么样的结论？

（1）发送时延 $\frac{10^7 \, \text{bit}}{100 \, \text{kb/s}} = 100 \, \text{s}$，传播时延 $\frac{1000 \, \text{km}}{2 \cdot 10^8 \, \text{m/s}} = 0.005 \, \text{s}$。

（2）发送时延 $\frac{10^3 \, \text{bit}}{1 \, \text{Gb/s}} = 10^{-6} \, \text{s}$，传播时延 $\frac{1000 \, \text{km}}{2 \cdot 10^8 \, \text{m/s}} = 0.005 \, \text{s}$。

结论：数据量大，发送速率低时，主要时延由发送时延引起；数据量少，发送速率高时，主要时延由传播时延引起。

1-18 假设信号在媒体上的传播速度为 $2.3 \times 10^8$ m/s。媒体长度 $l$ 分别为：
（1）10 cm（网络接口卡）
（2）100 m（局域网）
（3）100 km（城域网）
（4）5000 km（广域网）
现连续传输数据，试计算出当数据率为 $1$ Mb/s 和 $10$ Gb/s 时在以上媒体中正在传播的比特数。

（即求时延带宽积）

(1) $I = 10 \, \text{cm}$

传播时延 $t = \frac{10 \, \text{cm}}{2.3 \cdot 10^8 \, \text{m/s}} = 4.35 \cdot 10^{-10} \, \text{s}$。

$1 \, \text{Mb/s}$ 时：时延带宽积 $= (4.35 \cdot 10^{-10} \, \text{s}) \cdot 1 \, \text{Mb/s} = 4.35 \cdot 10^{-4} \, \text{bit}$。

$10 \, \text{Gb/s}$ 时：时延带宽积 $= (4.35 \cdot 10^{-10} \, \text{s}) \cdot 10 \, \text{Gb/s} = 4.35 \, \text{bit}$。

(2)(3)(4) 同理。

1-19 长度为 100 字节的应用层数据交给传输层传送，需加上 20 字节的 TCP 首部。再交给网络层传送，需加上 20 字节的 IP 首部。最后交给数据链路层的以太网传送，加上首部和尾部共 18 字节。试求数据的传输效率。数据的传输效率是指发送的应用层数据除以所发送的总数据（即应用数据加上各种首部和尾部的额外开销）。若应用层数据长度为 1000 字节，数据的传输效率是多少？

$$\frac{100}{100+20+20+18} = 63.3\%$$

$$\frac{1000}{1000+20+20+18} = 94.5\%$$

1-26 试解释以下名词：协议栈、实体、对等层、协议数据单元、服务访问点、客户、服务器、客户-服务器方式。

• 协议栈：主机或路由器中的协议层。
• 实体：任何可发送或接收信息的硬件或软件。
• 对等层：网络体系中，通信双方实现相同功能的层。
• 协议数据单元 (PDU)：对等层次之间传送的数据单位。
• 服务访问点 (SAP)：即同一系统内相邻两层实体交换信息的逻辑接口。
• 客户 (Client)：通信的应用进程中的服务请求方。
• 服务器 (Server)：通信的应用进程中的服务提供方。
• 客户-服务器方式 (C/S)：客户请求服务，服务器提供服务的通信方式。

1-28 假定要在网络上传送 1.5MB 的文件。设分组长度为 1KB，往返时间 RTT = 80ms。传送数据之前还需要有建立 TCP 连接的时间，这时间是 $2 \cdot RTT = 160ms$。试计算在以下几种情况下接收方收完该文件的最后一个比特需要的时间。

分组数量：
$$\frac{1.5 \, \text{MB}}{1 \, \text{KB}} = \frac{1.5 \cdot 2^{20} \, \text{B}}{2^{10} \, \text{B}} = 1536$$

(1) 数据发送速率为 10Mbit/s，数据分组可以连续发送。

发送时延：
$$t_1 = 1536 \cdot \frac{1 \, \text{KB}}{10 \, \text{Mbit/s}} = 1536 \cdot \frac{8 \, \text{Kb}}{10^7 \, \text{bit/s}} = 1.258 \, \text{s}$$

传播时延：
$$t_2 = \frac{\text{RTT}}{2} = \frac{80 \, \text{ms}}{2} = 40 \, \text{ms} = 0.04 \, \text{s}$$

处理时延：
$$t_3 = 0 \, \text{s}$$

总时延：
$$t = 2 \cdot RTT + t_1 + t_2 = 2 \cdot 0.08 \, \text{s} + 1.258 \, \text{s} + 0.04 \, \text{s} = 1.458 \, \text{s}$$

(2) 数据发送速率为 10Mbit/s，但每发送完一个分组后要等待一个 RTT 时间才能再发送下一个分组。

发送时延：
$$t_1 = 1536 \cdot \frac{1 \, \text{KB}}{10 \, \text{Mbit/s}} = 1.258 \, \text{s}$$

传播时延：
$$t_2 = \frac{\text{RTT}}{2} = 0.04 \, \text{s}$$

处理时延：
$$t_3 = (1536 - 1) \cdot RTT = 1535 \cdot 0.08 \, \text{s} = 122.8 \, \text{s}$$

总时延：
$$t = 2 \cdot RTT + t_1 + t_2 + t_3 = 0.16 \, \text{s} + 1.258 \, \text{s} + 0.04 \, \text{s} + 122.8 \, \text{s} = 124.258 \, \text{s}$$

(3) 数据发送速率极快，可以不考虑发送数据所需要的时间。但规定在每一个 RTT 往返时间内只能发送 20 个分组。

发送时延：
$$t_1 = 0 \, \text{s}$$

传播时延：
$$t_2 = \frac{\text{RTT}}{2} = 0.04 \, \text{s}$$

处理时延：
$$t_3 = \left\lfloor \frac{1536}{20} \right\rfloor \cdot RTT = 77 \cdot 0.08 \, \text{s} = 6.16 \, \text{s}$$

总时延：
$$t = 2 \cdot RTT + t_2 + t_3 = 0.16 \, \text{s} + 0.04 \, \text{s} + 6.16 \, \text{s} = 6.36 \, \text{s}$$

(4) 数据发送速率极快，可以不考虑发送数据所需要的时间。但在第一个 RTT 往返时间内只能发送一个分组，在第二个 RTT 内可以发送两个分组，在第三个 RTT 内可以发送四个分组。

第 $n$ 个 RTT 后，已经发送了 $2^n - 1$ 个分组。
由于 $2^{10} - 1 < 1536 < 2^{11} - 1$，则在第 11 个 RTT 之前就可以发送完。

总时延：
$$t = 2 \cdot RTT + 10 \cdot RTT + \frac{\text{RTT}}{2} = 2 \cdot 0.08 \, \text{s} + 10 \cdot 0.08 \, \text{s} + 0.04 \, \text{s} = 0.96 \, \text{s}$$

以下是对上述内容的进一步修改和整理：

1-29 有一个对点链路，长度为 50KM。若数据在此链路上的传播速率为 $2 \times 10^8 \, \text{m/s}$，试问链路的带宽为多少才能使传播时延和发送 100 字节的分组的发送时延一样大？如果发送的是 512 字节长的分组，结果又是如何？

设带宽为 $x \, \text{bps}$，则发送一个分组的发送时延为：
$$t_1 = \frac{100 \, \text{B}}{x \, \text{bps}} = \frac{800}{x} \, \text{s}$$

传播时延：
$$t_2 = \frac{50 \, \text{km}}{2 \times 10^8 \, \text{m/s}} = 2.5 \times 10^{-4} \, \text{s}$$

要使 $t_1 = t_2$，则：
$$\frac{800}{x} = 2.5 \times 10^{-4}$$
$$x = \frac{800}{2.5 \times 10^{-4}} = 3.2 \times 10^6 \, \text{bps}$$

若分组大小为 512 字节，则：
$$t_1 = \frac{512 \, \text{B}}{x \, \text{bps}} = \frac{4096}{x} \, \text{s}$$
$$\frac{4096}{x} = 2.5 \times 10^{-4}$$
$$x = \frac{4096}{2.5 \times 10^{-4}} = 1.6384 \times 10^7 \, \text{bps}$$

1-32 以 1 Gbit/s 的速率发送数据。试问在以距离或时间为横坐标时，一个比特的宽度分别是多少？

以时间为横坐标：
1 Gbit/s 即每秒传输 $10^9 \, \text{bit}$，则一个比特的时间宽度为：
$$T = \frac{1}{10^9} = 10^{-9} \, \text{s}$$

以距离为横坐标：
传播速率 $v = 2 \times 10^8 \, \text{m/s}$，则一个比特的距离宽度为：
$$D = v \cdot T = 2 \times 10^8 \, \text{m/s} \cdot 10^{-9} \, \text{s} = 0.2 \, \text{m}$$

1-34 主机 A 向主机 B 发送一个长度为 $10^7$ 比特的报文。中间要经过两个节点交换机，即一共经过三段链路。设每条链路的传输速率为 2 Mbit/s。忽略传播、处理和排队时延。

(1) 如果采用报文交换，即整个报文不分段，每台节点交换机收到整个的报文后再转发。问从主机 A 把报文传送到第一个节点交换机需要多少时间？从主机 A 把报文传送到主机 B 需要多长时间？

(2) 如果采用分组交换。报文被划分为 1000 个等长的分组，并连续发送。节点交换机能够边接受边发送。试问从主机 A 把第一个分组传送到第一个节点交换机需要的时间？从主机 A 把第一个分组传送到主机 B 需要多少时间？从主机 A 把 1000 个分组传送到主机 B 需要多少时间？

(3) 就一般情况而言，比较用整个报文来传送和用划分多个分组来传送的优缺点。

解答：
A -> 交换机 1 -> 交换机 2 -> B

(1) 报文交换：
第一段链路传输时长：
$$t_1 = \frac{10^7 \, \text{bit}}{2 \, \text{Mbps}} = 5 \, \text{s}$$

主机 A 到主机 B 的传输时长：
$$t = 3 \cdot t_1 = 3 \cdot 5 \, \text{s} = 15 \, \text{s}$$

(2) 分组交换：
单个分组大小：
$$\frac{10^7 \, \text{bit}}{1000} = 10^4 \, \text{bit}$$

单个分组到达交换机 1 的传输时延：
$$t_1 = \frac{10^4 \, \text{bit}}{2 \, \text{Mbps}} = 5 \times 10^{-3} \, \text{s}$$

单个分组到达主机 B 的传输时延：
$$t_2 = 3 \cdot t_1 = 3 \cdot 5 \times 10^{-3} \, \text{s} = 0.015 \, \text{s}$$

主机 A 到主机 B 的总传输时长（1000 个分组）：
$$t = t_2 + (1000 - 1) \cdot t_1 = 0.015 \, \text{s} + 999 \cdot 5 \times 10^{-3} \, \text{s} = 5.01 \, \text{s}$$

(3) 比较：

• 分组交换：

  • 优点：传输速度快；若某个分组出错，只需重传该分组；可以通过不拥堵的链路传输。
  • 缺点：缺少一个分组会导致无法重组报文；分组首部带来额外开销。

• 报文交换：

  • 优点：没有额外开销。
  • 缺点：若某个比特出错，需要重传整个报文。

1-35 主机 A 向主机 B 连续传送一个 600,000 比特的文件。A 和 B 之间有一条带宽为 1 Mbit/s 的链路相连，距离为 5000KM，在此链路上的传播速率为 $2.5 \times 10^8 \, \text{m/s}$。

(1) 链路上的比特数目的最大值是多少？
(2) 链路上每比特的宽度是多少？
(3) 若想把链路上每比特的宽度变为 5000KM，这时应把发送速率调整到什么数值？

解答：

(1) 链路上的比特数目的最大值：
传播时延：
$$t_{\text{传播}} = \frac{5000 \, \text{km}}{2.5 \times 10^8 \, \text{m/s}} = 0.02 \, \text{s}$$

时延带宽积：
$$\text{时延带宽积} = t_{\text{传播}} \cdot \text{带宽} = 0.02 \, \text{s} \cdot 1 \, \text{Mbit/s} = 0.02 \, \text{Mb} = 20,000 \, \text{bit}$$

(2) 链路上每比特的宽度：
时间宽度：
$$T = \frac{1}{1 \, \text{Mbit/s}} = 10^{-6} \, \text{s}$$

距离宽度：
$$D = v \cdot T = 2.5 \times 10^8 \, \text{m/s} \cdot 10^{-6} \, \text{s} = 250 \, \text{m}$$

(3) 若距离宽度 $D = 5000 \, \text{km}$，则时间宽度：
$$T = \frac{D}{v} = \frac{5000 \, \text{km}}{2.5 \times 10^8 \, \text{m/s}} = 0.02 \, \text{s}$$

发送速率：
$$\text{发送速率} = \frac{1 \, \text{bit}}{T} = \frac{1}{0.02} = 50 \, \text{bps}$$

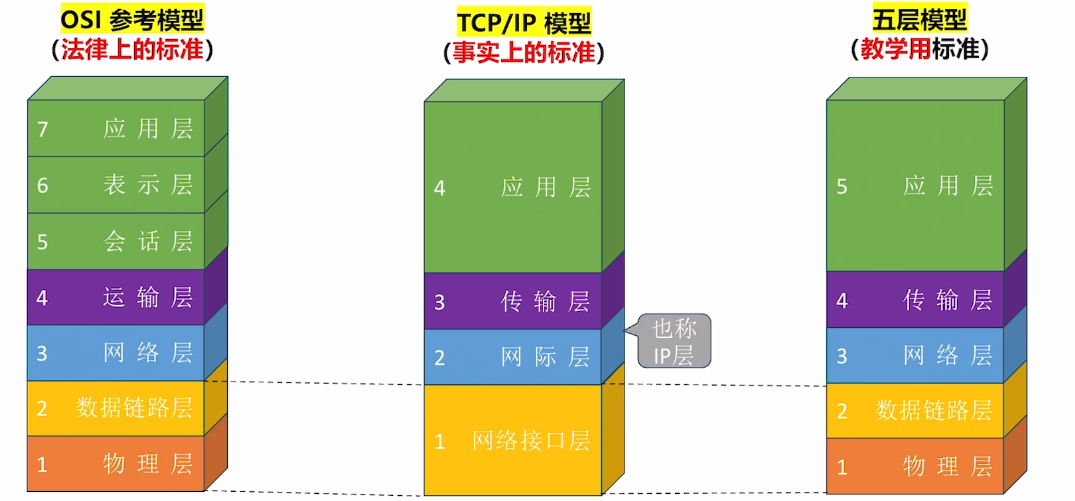
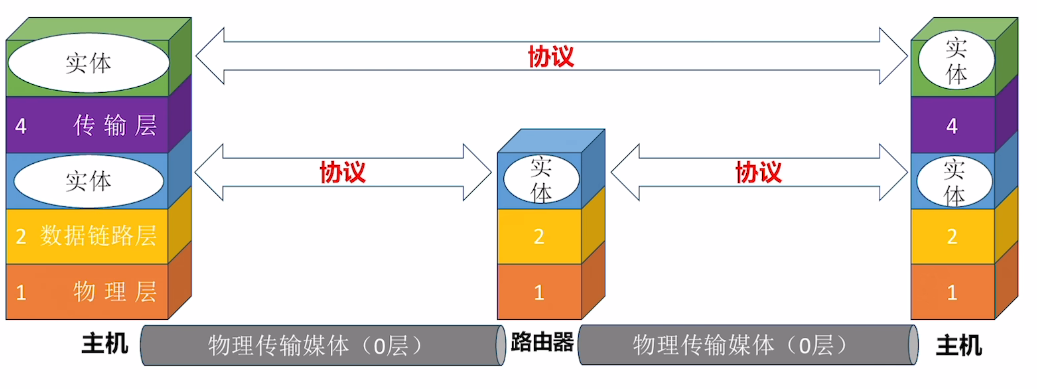
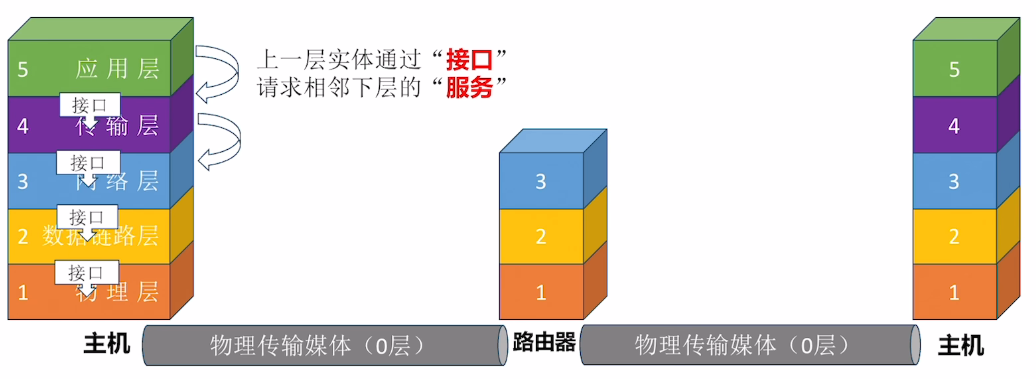
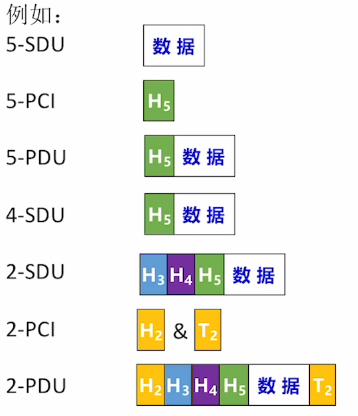
仅适用于有一定基础的读者

2025/1/5 XPIPI

第一章 Java概述

1.Java的语言特性：面向对象、平台无关性、多线程、垃圾自动回收机制、安全性

2.Java源文件拓展名为.java，通过编译指令javac后可得到扩展名为.class的字节码文件，字节码可通过运行指令java运行

3.用java命令运行程序不需要添加字节码文件拓展名.class

4.javadoc命令用于生成文档，javap命令用于反汇编，jar命令用于打包Java字节码文件，jdb为命令行式的调试工具

5.使用package来创建一个包

6.使用import来导入一个包，默认已导入java.lang包

第二章 Java语法基础

1.文档注释 / ... / 与多行注释 / / 区分

2.对象实例化时，若成员变量没有显式赋值，则取值为对应数据类型的默认值；若数组没有显式赋值，各元素都取默认值

3.引用数据类型的默认值为null

4.将浮点型转换为整型时，小数点后数据将被截掉，精度下降

5.不推荐用包装类的构造方法创建包装类对象，一般用包装类的valueOf()方法

6.用parseXxx(String s)将字符串转为基本类型，用valueOf(Xxx x)将基本数据类型转化为字符串

7.instanceof为二元运算符，判断左边是不是右边的类型

8.若精度不同，==运算结果也为false

9.&&和||会发生短路现象，&和|不会

10.使用带标签的break语句，应当再break所在循环的外层循环之前定义

11.abstract和final修饰符不能同时使用

12.方法重载的名字一定相同，参数列表一定不同，其它随意

13.多维数组声明并初始化的三种方式

int a[][]=new int[][]{{1,1,1},{2,2,2},{3,3,3}};
int a[][]={{1, 1, 1}, {2, 2, 2}, {3, 3, 3}}
{
    int[][] a = new int[3][3];
    a[0] = new int[]{1, 1, 1};
    a[1] = new int[]{2, 2, 2};
    a[2] = new int[]{3, 3, 3};
}

14.foreach只能遍历访问，不能修改也不能局部访问

第三章 面向对象基础

1.一般来说，成员变量和属性是一个意思，实例与对象是一个意思，创建对象和实例化对象是一个意思

2.类体中不能对成员变量进行操作，只能在代码块中进行操作

3.栈内存和堆内存 类的对象在堆中分配空间

4.既可以用类.Xxx也可以用对象.Xxx来访问类变量

5.类都至少有一个构造方法

6.在程序块中，变量遵循就近原则，即同名的局部变量可以屏蔽外部的成员变量

7.this()调用构造方法时必须放在第一行

8.访问权限：private<default<protected<public

9.类不能用private和protected修饰

10.调用System.gc()方法和Runtime.getRuntime.gc()来强制进行垃圾回收

11.finalize()方法由垃圾回收器调用，不要主动调用

12.Runtime类是一个单例类，通过getRuntime方法来获得这个对象

13.运行顺序：静态块->构造块->构造方法

14.构造块在每次调用构造方法时前都会运行一次

15.没有任何前缀后缀修饰只由大括号{}括起来的就是构造快

第四章 面向对象高级技术

1.Java采用类的单继承可多重继承，接口可以同时多实现

2.方法重写的方法名、参数列表、返回值必须一模一样，而且子类重写的方法访问权限必须大于等于父类

3.方法重写和方法重载是实现多态的重要形式。

4.super调用父类的构造方法也要放在第一句

5.所有类直接或间接继承java.lang.Object类，因此都有toString,equals,hashCode,clone,notify,notifyAll,wait等方法

6.final修饰的类不能被继承

7.一般用static final来修饰常量

8.局部变量声明后必须显式初始化

9.wait,notify,notifyAll,getClass()方法是final修饰的，不能被重写

10.向下转型转换后引用对象可以访问子类成员，而向上转型转换后引用对象不能访问不是重写的子类成员

具体原因点我可看

11.向下转型时，必须确保运行时类型确实是子类对象，否则会抛出 ClassCastException

因此，为了避免产生异常，可以使用instanceof运算符进行目标类型的判断

12.抽象类的子类如果是普通类，必须实现所有抽象类的抽象方法

13.抽象类可以含有属性、方法、构造方法、程序块等

14.抽象类可以没有抽象方法，也可以有非抽象方法

15.接口可以使用extends继承一个或者多个接口，但是不能继承类

16.接口中变量都是常量，必须显式初始化

17.接口中方法都是public abstract修饰

18.如果一个接口中只有一个抽象方法，这个接口称作函数式接口，在lambda表达式中可以用到

19.接口中可以有默认方法，用default修饰

20.如果一个类同时实现接口A和B，接口A和B中有相同的default方法，这时，该类必须重写接口中的default方法

21.如果子类继承父类，父类中有b方法，该子类同时实现的接口中也有b方法（被default修饰），那么子类会继承父类的b方法而不是继承接口中的b方法

22.接口中也可以有静态方法，用static修饰

23.一个类可以同时实现多个接口；一个类只能继承一个类，但是能实现多个接口；一个接口可继承多个接口。

24.充分利用接口可以降低程序各个模块之间的耦合度，提高系统的可拓展性和可维护性

25.内部类可以用static修饰为静态内部类，但是内部类的成员不能声明为static类型

26.内部类名不能与外部类同名

27.

实例化静态内部类对象的模板是： 外部类类名.内部类类名 xxx = new 外部类类名.内部类类名()

实例化非静态内部类对象的模板是：外部类类名.内部类类名 xxx = 外部类对象名.new 内部类类名()

OuterStaticClassName.InnerStaticClassName objectName = new OuterStaticClassName.InnerStaticClassName();
OuterClassName.InnerClassName objectName = new OuterClassName().new InnerClassName();

28.局部内部类定义在方法内，作用域在方法里

29.局部内部类不能使用访问控制修饰符，也不能用static修饰

30.匿名内部类因为没有类名，所以不能复用，不能实例化

第五章 Java API

1.String的subString方法取的是左闭右开的区间，StringBuffer的delete方法也是

2.StringBuffer支持多线程，也是线程安全的

3.StringBuffer的默认缓冲区容量为16个字符

4.StringBuilder线程不安全，但是支持链式操作

5.拼接字符串效率：StringBuilder > StringBuffer > String

6.toString方法在没有重写时默认是返回 getClass().getName() + "@" +Integer.toHexString(hashCode());

7.String类重写了toString 方法

public String toString()  return this

8.String类重写了equals和hashCode方法，但是StringBuffer类和StringBuilder没有重写，equals方法仍然是比较两个对象的地址是否相等

9.StringBuffer类和StringBuilder类用于字符串追加、插入、删除、反转等操作，且其内容可以改变，且字符串拼接的效率明显比String类高

10.java.util.StringTokenizer类用于分割字符串

11.时间与日期相关的三个重要的类：Date、Calendar、DateFormat

12.Date类返回的时间是以毫秒ms为单位的

13.Calendar.DAY_OF_WEEK返回星期几

14.规定的标准时间格式：

日期：yyyy-MM-dd;

时间：HH:mm:ss;

带毫秒的时间：HH:mm:ss.SSS;

日期和时间：yyyy-MM-dd'T'HH:mm:ss; 日期与时间之间用'T'隔开

带毫秒的日期和时间：yyyy-MM-dd'T'HH:mm:ss.SSS

15.Local系列的类(LocalDateTime LocalDate LocalTime)都有parse方法用于进行将字符串转为相应的日期和时间类型

16.Instant.now()从系统时钟获得当前瞬时

17.Duration类和Period都是计算一个时间段，不同的是Duration类基于时间值，而Period类基于日期类，都使用以下方法创建：

Duration duration = Duration.between(time1,time2);

Period period = Period.between(time1.toLocalDate(),time2.toLocalDate());

18.DateFormat是一个抽象类，SimpleDateFormat是其实现类

19.通过SimpleDateFormat的format方法将一个Date对象转化为一个相应格式的字符串，回转用parse方法

20.Math.random()方法生成一个(0.0,1.0)的随机数

21.Random类在构建随机数生成器时可以自定义一个种子，也可以通过无参数来随机一个随机数种子

22.Random类的nextInt方法如果无参数则返回一个任意范围的整数，如果有参数X则返回一个[0,X]的整数

23.基本数据类型都有其对应的包装类

24.将十进制转化为二进制可以用包装类的toBinartString(int i)方法，转化其它进制同理

25.包装类才可以使用泛型，而基本数据类型不可以

26.基本数据类型比包装类占用的内存空间更小，是一种轻量级的

27.在小数点需要保留指定位数时，建议用参数类型为String的构造方法构造BigDecimal对象

28.System类代表当前Java程序的运行平台，Runtime类表示当前JVM的工作信息

29.System的类变量中：out和err属于PrintStream类型，in属于InputStream类型

30.另外，InputStream提供了read方法接受字节数据，因此可以用System.in.read()来读取单个字符

31.打开一个计算器可以用Runtime类的exec方法，记得要捕获异常

32.用Pattern类对正则表达式进行编译，用Matcher类在给定Pattern实例的模式控制下进行字符串的匹配工作

33.String也提供了matches方法，可以使用正则表达式进行匹配

34.Java集合由两个根接口派生：单列结构Collection和双列结构Map

35.List和Set是Collection其中两个应用最为广泛的子接口，List元素有序且可重复，Set元素无序且不能重复

36.集合遍历的方式有以下五种。

基本循环如for/while循环：这种方式功能上最为强大，遍历时也可以修改、删除元素。

Iterator:比较简便的遍历方式，遍历时可以删除元素。

ListIterator:Iterator的子接口，专门用于List集合的遍历，支持双向遍历。

Enumeration:遍历Properties等双列集合的方式，遍历时不能修改、删除元素。

foreach:遍历方式上最为简便，同时功能上也最弱，遍历时不能修改、删除元素。

除了基本循环之外，其他方式遍历时，不可以通过集合对象的方法操作集合中的元素，因为会发生ConcurrentModificationException异常。Iterator提供的方法是有限的，只能对元素进行判断、取出、删除的操作，如果想要其他的操作如添加、修改等，就需要使用其子接口ListIterator。该接口只能通过List集合的listIterator方法获取。Enumeration和foreach方式功能上更为单一，遍历时不能修改、删除元素。

37.ArrayList效率没有数组高，但是可以动态改变大小，可以很方便添加删除修改元素

38.从集合中取出元素进行强制转换可能带来隐患，所以一般使用泛型，例如：

ArrayList<String> list = new ArrayList<String>();

39.TreeSet类在实现Set接口的同时，也实现了SortedSet接口，保证元素为升序

40.HashSet类在使用自定义类的时候，必须重写hashCode和equals方法

41.TreeSet本质上是一个自平衡二叉搜索树，即红黑树的实现 操作元素的时间复杂度为O(logN)

42.基本数据类型对应的包装类，String类都实现了Comparable接口，因此添加到TreeSet中可以按照自然排序的方式进行排序

43.添加其它引用类型的元素，必须实现Comparable接口，重写CompareTo方法，否则TreeSet无法排序，产生ClassCastException异常

44.Map中Key和Value都可以是null，但是Key一定是唯一的

45.Map接口的方法中

keySet 返回包含所有键值的Set集合

values返回Map中所有值组成的Collection集合

entrySet返回所有键值对组成的Set集合

46.HashMap类似于HashTable，但他是不同步的

47.SortedMap接口也有一个实现类TreeMap，对所有的键值对按照键进行排序，同时也需要实现Comparable接口

48.Properties类称为属性列表，继承于Hashtable类

49.泛型方法的类型参数可以用来声明返回值的类型，注意类型参数只能代表引用型类型，不能是基本数据类型

50.Lambda表达式中，一个参数可以不用圆括号，代码只有一个语句可以不用大括号，但是箭头一定有

51.Lambda表达式在很多场合下可以代替匿名内部类

第六章 异常处理机制

1.Throwable类是异常顶层父类，两个直接子类Error类和Exception类

2.Exception类分为运行时异常和编译时异常，编译时异常必须手动处理

3.getMessage方法可以返回异常对象的详细信息，toString方法可以返回异常对象的简短描述，printStackTrace方法将异常及其追踪输出至标准错误流

4.try-catch-finally语句中，finally一定会执行，而且返回值会覆盖掉前面代码的返回值，所以一般用来关闭字节流之类的收尾操作

5.应把捕获子类异常的catch语句放在前，捕获父类异常的语句放在后

6.return语句出现在catch语句内，直接退出方法，而不是回到异常抛出点

7.finally语句不是必须的

8.在方法名后面用throws声明一个或者多个异常，交给调用这个方法的程序来处理异常

9.自定义异常对象无法由系统产生并抛出，所以需要手动生成异常对象并抛出，使用throw语句

10.throw语句抛出的是异常对象，而不是一个异常类，所以需要先实例化异常类再抛出

11.自定义异常类必须继承Throwable类或者其子类，一般不继承Error类

12.当自定义异常类继承RuntimeException及其子类时，是运行时异常，在程序中可以不捕获并处理他

第七章 Java I/O流

1.数据从外部流向程序：输入流 数据从当前程序流向外部：输出流

2.Stream结尾就是字节流，Reader/Writer结尾就是字符流

3.节点流直接在输入输出媒介之上建立，过滤流在节点流类的基础上对节点流功能进行拓展

4.无论是节点流还是字符流，进行读写都是顺序读写的

5.但是也提供了一个随机读写类RandomAccessFile，也在java.io包中

6.标准输入输出流 System类的 in,out,err

7.File类只能对文件本身进行操作，即创建文件、删除文件、返回路径、文件是否存在等

8.File类也可以查看系统磁盘空间信息，以字节为单位返回

9.实现FilenameFilter接口的类实例可以用于过滤文件名，实现抽象方法:

boolean accept(File dir,String name)

10.字节流可以用来处理任何文件，而处理文本文件一般使用字符流

11.InputStream类和OutputStream类是字节流的顶层抽象父类

12.最常用的两个字节流类：FileInputStream和FileOutputStream 通过read和write方法可以对文件数据进行操作

13.实例化FileInputStream，输入参数需要为File类对象或者是一个字符串代表的文件地址

14.I/O流在不使用之后一定要用close关闭

15.FileInputStream找不到文件会抛出FileNotFoundException异常，而FileOutputStream找不到文件会创建一个对应的文件

16.FileOutputStream遇到一个只读文件的时候会抛出IOException异常

17.过滤字节流相当于一个过滤器，必须连接到一个节点流对象，例如

FileInputStream fis = new FileInputStream("xx.txt");
DataInputStream dis = new DataInputStream(fis);

18.FilterInputStream类和FilterOutputStream类为抽象类，

FilterInputStream有三个子类BufferedInputStream,DataInputStream,PushbackInputStream

FilterOutputStream有三个子类BufferedOutputStream,DataOutputStream,PrintStream

19.FilterInputStream类和FilterOutputStream类分别重写了InputStream类和OutputStream类的所有方法

20.BufferedInputStream为缓冲字节流，提高了读写效率，默认缓冲区为32B

21.缓冲输出字节流链接到节点输出流OutputStream

22.在使用缓冲字节流时，一定要在最后使用flush方法强制清空缓冲器，将最后没填满缓冲区的数据输出到节点输出流

23.PushbackInputStream顾名思义，用来需要对数据进行分析的时候，可能需要超前读入一个字节进行判断，然后再从缓冲区将字节返回

24.PushbackInputStream在顶层父类的基础上增加了unread方法，默认返回一个由低8位构成的字节

25.回退过程中如果缓存区满了就不能进行回退unread操作，否则产生IOException异常

26.PrintStream类捕获抛出IOException，而是通过checkError方法来设置测试的内部标志来检测异常

27.PrintStream可以在写入字节数组之后自动调用flush方法

28.实际上out是System类的一个PrintStream类型的类变量，可以调用println和print方法

29.管道字节流一般用于在互联网上传输数据，必须输入输出流同时使用

30.PipedInputStream类和PipedOutputStream类提供了两种方法进行输入输出流的链接

一个是使用connect方法

一个是在实例化管道流对象时进行链接

31.顺序输入流SequenceInputStream可以将几个输入流按顺序连接起来，也就是将多个不同的输入流统一为一个输入流

32.通过将一个Java类实现Serializable接口来表明这个类的对象是可以被序列化的，以此对该对象进行持久化，并可以使用对象流进行操作

33.序列化只能保存对象的实例变量，不能保存任何类的方法和类变量

34.对于用transient关键字标明的瞬时成员变量，对象也不会保存其状态

35.线程对象或流对象的状态是瞬时的，必须用transient修饰，否则编译出错

36.对象流ObjectInputStream和ObjectOutputStream类分别实现了ObjectInput和ObjectOutput接口

37.对象流的构造方法和使用方法于数据流的构造方法以及使用方法基本相同

38.利用对象流输入输出对象时，也需要与其它字节流作为节点流连接起来使用

39.Java采用16位的二进制字符编码方案：Unicode

40.Reader类和Writer类是所有字符流的顶层抽象父类

41.Reader类的ready方法可以用于判断是否准备读取此流

42.Writer类追加字符到字符流的方法为append

43.转换类：InputStreamReader和OutputStreamWriter类

用于处理字节流转换字符流转换

44.实例化转换类对象的方法：

InputStreamReader(InputStream in,String charsetName)

charsetName为可选的指定字符集

45.缓冲字符流BufferedReader和BufferedWriter和缓冲字节流差不多，但是提供了readline和newline方法，可以一行一行的进行操作，而且在行操作时候会使用到行结束标志

46.因为字节流的兼容性不好，操作Unicode编码的文件一般使用文件字符流FileReader和FileWriter

47.文件输出流在实例化时可以选择参数是否为追加模式

FileWriter(File file,boolean append)

48.管道字符流PipedRead和PipedWriter也必须同时使用

49.PrintWriter类类似于PrintStream，可以对基本数据类型进行处理，还可以接受Writer对象作为输出对象

50.RandomAccessFile可以实现随机读写文件，注意是读写都可以；使用getFilePointer方法返回当前指针位置，使用seek方法调整指针位置

51.RandomAccessFile操作文件的模式

r：制度

rw：读写

rws：同步读写，同步写文件内容和文件属性

rwd：数据同步读写，同步写文件内容，不修改文件属性

52.

InputStream和OutputStream是所有字节流类的“祖先”，读写数据的单位是字节。

Reader和Writer是所有字符流类的“祖先”，读写数据的单位是字符。

File类用于创建、删除指定的文件或目录，并且可以获取该文件或目录的属性信息及所在磁盘的信息等，但File类不能打开文件。

FileInputStream/FileOutputStream、FileReader/FileWriter和RandomAccessFile是处理本地文件的类。可以对文件进行读写操作，RandomAccessFile还可以随机地读写指定文件。

BufferedInputStream/BufferedOutputStream和BufferedReader/BufferedWriter提供了缓冲区，达到一定数量时再送到目的文件，以减少阻塞次数，提高读写效率，适合读写大文件。

PipedInputStream/PipedOutputStream和PipedReader/PipedWriter是管道流，要求管道输入流和管道输出流同时使用，适合网络编程。

HeyHey说在前头

本篇将会结合个人理解，对一些我觉得值得讲的代码进行部分注释

基于严蔚敏版《数据结构(C语言版)》

后面想到什么了再补充

——XPIPI

第二章 线性表

算法2.4 顺序线性表的插入

书中算法

Status ListInsert_Sq(SqList &L,int i,ElemType e)
    // L 线性表 i在第i个位置插入 e需要插入的元素
    // 在顺序线性表L中第i个位置之前插入新的元素e
    // i的合法值为 1 <= i <= ListLength.Sq(L) + 1
    // ①验证合法性
    if(i < 1 || i > L.length + 1) {
        return ERROR;
    }
    // ②存储空间满了 需要增加分配的空间
    if(L.length >= L.listsize){
        // 注意：类似malloc，realloc在调用头文件stdlib.h后返回值为 (void *) 这里使用 (ElemType *) 强制转化为我们需要的数据类型的指针
        newbase = (ElemType *)realloc(L.elem,L.listsize+LISTINCREMENT) * sizeof(ElemType);
        // 此处的LISTINCREMENT为之前宏定义过的
        if(!newbase){
            exit(OVERFLOW);
            /*
            OVERFLOW为math.h的一个宏定义，值为3 也即exit(3); 表示运算溢出,存储分配失败
            当然，你也可以自己宏定义OVERFLOW的值
            */
            // 存储分配成功后进行新地址的赋值操作
               L.elem = newbase;
            L.listsize += LISTINCREMENT;
        }
        // ③找插入位置为q 
        q = &(L.elem[i-1]);
        // 将q之后的元素全部右移
        for(p = &(L.elem[L.length-1]);p >= q;--p){
            *(p+1) = *p;
        }
        // 在q这个位置插入e，并增加表长
        *q = e;
        ++L.length;
        return OK;
    }

实现代码

//函数状态码定义
#define TRUE        1
#define FALSE       0
#define OK          1
#define ERROR       0
#define INFEASIBLE -1
#define OVERFLOW   -2
 
typedef int Status;
 
//顺序表的存储结构定义
#define LIST_INIT_SIZE  100
#define LISTINCREMENT   10
typedef int ElemType;

typedef struct{
    ElemType *elem;
    int length;
    int listsize;
}SqList;

Status ListInsert_Sq(SqList &L,int pos,ElemType e){
    if(pos < 1 || pos > L.length + 1) return ERROR;
    if(L.length >= L.listsize){
        int *newbase = (ElemType*)realloc(L.elem,(L.listsize + LISTINCREMENT) * sizeof(ElemType));
        if(!newbase) return OVERFLOW;
        L.elem = newbase;
        L.listsize += LISTINCREMENT
    }
    for(int i = L.length;i >= pos - 1;--1){
        L.elem[i + 1] = L.elem[i];
    }
    L.elem[pos-1] = e;
    L.length++;
    return OK;
}

算法2.5 顺序线性表的删除

书中算法

Status ListDelete_Sq(SqList &L,int i,ElemType &e){
    // L 线性表 i在第i个位置删除 e被删除的元素（此处为引用传递)
    // 在顺序线性表L中删除第i个元素，并用e返回值
    // i的合法值为 1 <= i <= ListLength.Sq(L)
    // ①验证合法性
    if(i < 1 || i > L.length) {
        return ERROR;
    }
        // 找删除位置为p
        p = &(L.elem[i-1]);
        // 将p这个位置的值赋给e *p解引用
        e = *p;
        // 表尾元素标记 左边移动一个
        q = L.elem+L.length-1;
        // 将p之后的元素全部左移
        for(++p;p <= q;++p){
            *(p-1) = *p;
        }
        // 减少表长
        --L.length;
        return OK;
}

实现代码

//函数状态码定义
#define TRUE        1
#define FALSE       0
#define OK          1
#define ERROR       0
#define INFEASIBLE -1
#define OVERFLOW   -2
 
typedef int Status;
 
//顺序表的存储结构定义
#define LIST_INIT_SIZE  100
#define LISTINCREMENT   10
typedef int ElemType;

typedef struct{
    ElemType *elem;
    int length;
    int listsize;
}SqList;

Status ListDelete_Sq(SqList &L,int pos,ElemType &e){
    if(pos < 1 || pos > L.length) return ERROR;
    e = L.elem[pos-1];
    for(int i = pos - 1;i < L.length - 1;++i){
        // 不要用L.elem[i-1] = L.elem[i] 因为是从i开始的，如果i=pos-1=0的情况下会出错
        L.elem[i] = L.elem[i+1];
    }
    L.length--;
    return OK;
}

算法2.7 顺序表的合并

书中算法

void MergeList_Sq(SqList La,SqList Lb,SqList &Lc){
    // 原顺序线性表La、Lb为非递减排列顺序表 Lc为结果顺序表
    // 合并后Lc也为非递减排列顺序表（即升序）
    // 用pa和pb表示La和Lb的基址
    pa = La.elem;pb = Lb.elem;
    // 合并后Lc的大小
    Lc.listsize = Lc.length = La.length + Lb.length;
    // 给Lc分配内存 并用pc表示Lc的基址
    pc = Lc.elem = (ElemType *)malloc(Lc.lisesize * sizeof(ElemType));
    // 分配内存溢出情况
    if(!Lc.elem){ // 这里用!pc也是一样的
        exit(OVERFLOW);
    }
    // 用pa_last和pb_last表示La和Lb的最后一个元素
    pa_last = La.elem + La.length - 1;
    pb_last = Lb.elem + Lb.length - 1;
    // 比较当前pa和pb大小，并插入到Lc中
    while(pa <= pa_last && pb <= pb_last){ // La和Lb都还有元素剩余
        if(*pa <= *pb){
            *pc++ = *pa++;
            /* 看不懂？其实这一句等价于：
                *pc=*pa;
                pc++;
                pa++;
                也就是赋值，并分别移动指针
                下面同理
            */
        }
        else *pc++ = *pb++;
    }
    // La和Lb有一个元素插入完了变成空表了 将另外一个还有元素的表直接全部插入到Lc后面
    while(pa <= pa_last) *pc++ = *pa++;
    while(pb <= pb_last) *pc++ = *pb++;
}

实现代码

//函数状态码定义
#define TRUE        1
#define FALSE       0
#define OK          1
#define ERROR       0
#define INFEASIBLE -1
#define OVERFLOW   -2
 
typedef int Status;
 
//顺序表的存储结构定义
#define LIST_INIT_SIZE  100
#define LISTINCREMENT   10
typedef int ElemType;

typedef struct{
    ElemType *elem;
    int length;
    int listsize;
}SqList;

// 冒泡排序 还记得怎么写吗
Status ListSort_Sq(SqList &L){
    for(int i = 0;i < L.length - 1;++i){
        for(int j = 0;j < L.length - 1 - i;++j){
            if(L.elem[j] > L.elem[j+1]){
                swap(L.elem[j],L.elem[j+1]);
            }
        }
    }
    return OK;
}

// 本体在这儿
// 默认我们这里的La Lb已经排序好了（升序）
// !!这里是包含去重操作的 代码自己看
void MergeList_Sq(SqList La,SqList Lb,SqList &Lc){
    // i对应La j对应Lb k对应Lc
    int i = 0, j = 0, k = 0;
    Lc.elem = (ElemType*)malloc((La.length+Lb.length)*sizeof(ElemType));
    if(!Lc.elem) return OVERFLOW;
    while(i < La.length && j < Lc.length){
        if(La.elem[i] < Lb.elem[j]){//当La的i号元素比Lb的j号元素小
            if(k == 0 || Lc.elem[k-1] != La.elem[i]) {
                // 条件：如果 L3 是空表 (k == 0) 或 L3 的最后一个元素不等于 L1.elem[i]
                // 满足这个条件才加入这个元素 达成去重效果√
                Lc.elem[k++] = La.elem[i];
            }
            // 满不满足去重条件La都要移动到下一个元素 i++
            i++;
        }else if (La.elem[i] > Lb.elem[j]) {//以下同理
            if (k == 0 || Lc.elem[k - 1] != Lb.elem[j]){
                Lc.elem[k++] = Lb.elem[j];
            }
            j++;
        }else{//当La的i号元素比Lb的j号元素相等
            if (k == 0 || Lc.elem[k - 1] != La.elem[i]){
                // 满足条件后，随意添加其中一个
                Lc.elem[k++] = La.elem[i];
            } 
            i++;j++;
        }
    }
    // La或Lb还没空
    while(i < La.length){
        if(k == 0 || Lc.elem[k-1] != La.elem[i]) {
            Lc.elem[k++] = La.elem[i];
        }
        i++;
    }
    while(j < Lb.length){
        if(k == 0 || Lc.elem[k-1] != Lb.elem[i]) {
            Lc.elem[k++] = Lb.elem[i];
        }
        j++;
    }
    return OK;
    /*
    最终效果：
    合并两个有序线性表；
    去除重复元素；
    保持结果有序
    */
}

算法2.9 单链表的插入

书中算法 带头节点 i前插入

Status ListInsert_L(LinkList &L,int i,ElemType e){
    // 在带头节点的单链线性表L中第i个位置之前插入元素e
    // 将L赋给p 此时p代表头指针
    p = L;
    // j用于计数 从0开始
    j = 0;
    while(p && j < i-1){//p不为NULL且j比i-1小
        p = p->next;
        ++j;
        // 不断右移，直到到i-1结点结束
    }
    if(!p || j > i - 1){
        // 两种情况：1.i比表长+1还大 p遍历到表尾最后指向NULL 2.i小于1 j>i-1 将一直为true
        return ERROR;
    }
    // 生成新节点s
    s = (LinkList)malloc(sizeof(LNode));
    s->data = e;
    // 将s插入到L中 注意顺序不可变化
    s->next = p->next;
    p->next = s;
}

实现代码

#define ERROR 0 
#define OK 1
typedef int Status;
typedef int ElemType;

typedef struct LNode
{
    ElemType data;
    struct LNode *next;
 } LNode ,*LinkList;

Status ListInsert_L(LinkList &L,int i,ElemType e){
    LNode *p = L;
    // 也可以是 LinkList p = L
    int j = 0;
    while(p && j < i-1){
        p = p->next;
        ++j;
    }
    if(!p || j > i - 1) return ERROR;
    LNode *s = (LinkList)malloc(sizeof(LNode));
    s->data = e;
    s->next = p->next;
    p->next = s;
    return OK;
}

算法2.10 单链表的删除

书中算法

Status ListDelete_L(LinkList &L,int i,ElemType &e){
    // 在带头节点单链线性表L中，删除第i个元素，并由e返回对应值
    p = L;j = 0; // p代表头指针 j为计数器
    while(p->next && j < i-1){ //p->next不为NULL且j比i-1小
        p = p->next;
        ++j;
        //找到第i个结点后，这个时候p是第i个结点的前驱
    }
    if(!(p->next) || j > i-1){
        // 两种情况：1.对应i元素不存在 p遍历到表尾最后指向NULL 2.i小于1 j>i-1 将一直为true
        return ERROR;
    }
    // 指针q指向需要删除的元素 下面两行顺序不可换
    q = p->next;
    // 被删除元素的前驱的后驱更改为被删除元素的后驱
    p->next = q->next;
    // 提取被删除的值
    e = q->data;
    // 释放结点内存
    free(q);
    return OK;
}

实现代码

#define ERROR 0 
#define OK 1
typedef int Status;
typedef int ElemType;

typedef struct LNode
{
    ElemType data;
    struct LNode *next;
 } LNode ,*LinkList;

Status ListDelete_L(LinkList &L,int i,ElemType &e){
    LNode *p = L;
    int j = 0;
    while(p->next && j < i-1){
        p = p->next;
        ++j;
    }
    if(!(p->next) || j > i-1) return ERROR;
    LNode *q = p->next;
    p->next = q->next;
    e = q->data;
    free(q);
    return OK;
}

算法2.12 单链表的归并

书中算法

void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
    // La Lb 元素非递减排列（即递增）
    // 归并得到的新Lc也为非递减排列 链表操作均为引用
    // pa和pb用来表示La和Lb的首元结点
    pa = La->next;pb = Lb->next;
    // 用La的头结点作为Lc的头结点 当然你用Lb的也行:)
    Lc = pc = La;
    while(pa && pb){// pa和pb都没指向空
        if(pa->data <= pb->data){// pa指向元素值小于或等于pb指向元素值
            // 将pc指向结点的后驱改为pa指向结点
            pc->next = pa;
            // 将pc指向结点改为pa
            pc = pa;
            // 移动pa指针到下一个元素
            pa = pa->next;
            // 本质上可以理解成插入操作
        }else{
            pc->next = pb;
            pc = pb;
            pb = pb->next;
        }
        // 类似于顺序表 可能存在剩余元素 因为链表的性质可以利用三目运算符
        // 这里的pa如果是空的话是NULL 运行：pc->next = pb 反之运行：pc->next = pa
        pc->next = pa?pa:pb;
        free(Lb); //释放Lb头结点 如果前面用Lb当头结点了这里就释放La头结点
    }
}

实现代码

typedef int ElemType;

typedef struct LNode{
    ElemType data;
    struct LNode *next;//定义next为指向结构体LNode的指针
}LNode,*LinkList;
//LinkList也为一个指向结构体的指针   相当于 using LinkList = *LNode;

void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
    LinkList pa,pa,pc;
    pa = La->next;
    pb = Lb->next;
    Lc = pc = La;
    while(pa && pb){
        if(pa->data <= pb->data){
            pc->next = pa;
            pc = pa;
            pa = pa->next;
        }else{
            pc->next = pb;
            pc = pb;
            pb = pb->next;
        }
    }
    pc->next = pa?pa:pb;
    free(Lb);
}

第三章 栈和队列

栈的入栈与出栈

// 顺序栈的入栈
Status Push(SqStack &S,SElemType e){
    // 元素e入栈 先检查栈是否已满
    if(S.top - S.base >= S.stacksize){ //栈满条件
        // 若栈满，则重新分配存储空间
        S.base = (SElemType*)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(SElemType));
        // 当然也要考虑溢出导致分配失败情况
        if(!S.base) exit(OVERFLOW);
        // 移动栈顶指针到新的地址
        // 因为重新分配的S.base地址发生了改变 所以这个时候S.top也要跟着改变
        // 此时还没入栈 所以top指针就是指向扩充前的最大的那个元素
        S.top = S.base + S.stacksize;
        // 扩充后，栈的容量也要增加
        S.stacksize += STACKINCREMENT;
    }
    // 如果栈没满，或者经过扩充后 在栈顶添加元素e
    // 由于top指向的是栈顶的下一个位置 所以先将e压入栈顶 top指针再+1
    *S.top++ = e;
    // 等效为：*S.top = e; S.top++;
    return OK;
}

// 顺序栈的出栈
Status Pop(SqStack &S,SElemType &e){
    // 出栈一个元素，用e返回这个值 当然要先检查栈是否为空栈
    if(S.top == S.base){ // 判断空栈条件
        return ERROR;
    }
    // 同理，我们先给e赋值，然后top指针再-1
    // 栈容量不变
    e = *--S.top;
    // 等效为： e = *S.top; S.top--;
    return OK;
}

代码实现

#define OK 1
#define ERROR 0
#define OVERFLOW -2

#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
// define语句加分号是允许的（编译通过）但可能会出现问题 所以不推荐
typedef int SElemType;
typedef int Status;

typedef struct{
    SElemType *base;
    SElemType *top;
    int stacksize;
}SqStack;

Status Push(SqStack &S,SElemType e){
    if((S.top - S.base) >= S.stacksize){
        S.base = (SElemType*)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(SElemType));
        if(!S.base) exit(OVERFLOW);
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *S.top = e;
    S.top++;
    return OK;
}

Status Pop(SqStack &S,SElemType &e){
    if(S.top == S.base) return ERROR;
    e = *S.top;
    S.top--;
    return OK;
}

算法3.1 栈的应用：进制转换

书上代码

void conversion(){
    // 对于任意一个非负十进制整数，打印输出与其等值的八进制数
    // 原理：取商留余法
    InitStack(S);
    // 输入一个非负十进制整数N
    scanf("%d",N);
    // 入栈，得到八进制数序列
    while(N){ // N没被除成0前一直运行
        // 把当前的N mod 8入栈
        Push(S,N % 8);
        // 每次入栈一个数 N = N/8
        N /= 8;
    }
    // 出栈并打印结果
    while(!(StackEmpty(S)){
        Pop(S,e);
        printf("%d",e);
    }

}

代码实现

一个十进制 -> X进制的示例：

#define OK 1
#define ERROR 0
#define OVERFLOW -2

#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10

typedef int SElemType;
typedef int Status;

typedef struct{
    SElemType *base;
    SElemType *top;
    int stacksize;
}SqStack;

Status InitStack(SqStack &S)
Status Push(SqStack &S,SElemType e);
Status Pop(SqStack &S,SElemType &e);
Status StackEmpty(SqStack &S);

void conversion(){
    // 输入需要转换为几进制
    cin >> X;
    // 输入需要转换的数字
    cin >> num;
    InitStack(S);

    char ch[16] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
    while(num){
        Push(S,num % X);
        num /= X;
    }
    
    int e;
    while(!StackEmpty(S)){
        Pop(S,e);
        cout << e << " ";
    }
    cout << endl;
}

队列的入队和出队

// 一种链队列
Status EnQueue(LinkQueue &Q,QElemType e){
    // 将元素e插入到队尾 入队
    // 动态申请空间
    p = (QueuePtr)malloc(sizeof(QNode));
    // 存储分配失败
    if(!p) exit(OVERFLOW);
    // p赋值并next指向NULL（作为新的队尾元素)
    p->data = e;
    p->next = NULL;
    // p入队
    Q.rear->next = p;
    // 移动队尾指针
    Q.rear = p;
    return OK;
}

Status DeQueue(LinkQueue &Q,QElemType &e){
    // 若队列不为空，将Q的队头元素出队，并用e返回其值
    // 首先判断是否为空
    // 判断队列是否为空有三种方法，这里使用front=rear来判断，还有使用标记位flag和计数器count的方法
    if(Q.front == Q.rear) return ERROR;
    // 因为这里是链队列，指针p为头指针指向的下一个元素，也即首元元素(此时的队头)
    p = Q.front->next;
    // 此时p指向为即将出队的元素
    e = p->data;
    // 改变队列头指针指向的元素
    // 也可以写成 Q.front->next = Q.front->next->next 这两种等效
    Q.front->next = p->next;
    // 特殊情况：如果此时队尾元素也是即将出队的元素p 就说明这个队列只有一个元素 出队后将队列置空
    if(Q.rear == p) Q.rear = Q.front;
    // 出队操作后释放p
    free(p);
    return OK;
}

代码实现

#define OK 1
#define ERROR 0
#define OVERFLOW -2

typedef int QElemType;
typedef int Status;

typedef struct QNode{
    QElemType data;
    struct QNode *next;
}QNode,*QueuePtr;
typedef struct{
    QueuePtr front,rear;
}LinkQueue;

Status EnQueue(LinkQueue &Q, QElemType e) {
    QueuePtr p = (QueuePtr)malloc(sizeof(QNode));
    if (!p)
        exit(OVERFLOW);
    p->data    = e;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
    return OK;
}

Status DeQueue(LinkQueue &Q, QElemType &e) {
    if (Q.rear == Q.front)
        return ERROR;
    QueuePtr p = Q.front->next;
    e = p->data;
    Q.front->next = p->next;
    if (Q.rear == p)
        Q.rear = Q.front;
    free(p);
    return OK;
}

第四章 串

串的模式匹配算法 算法4.5 4.6 4.7

我们都知道子串的定位操作通常称作串的模式匹配，一般来说常用的有BF算法(也称蛮力法）和KMP算法两种实现方式，其中

BF算法：时间复杂度O(n*m) KMP算法：时间复杂度(n+m)

BF算法伪代码

int Index(SString S,SString T,int pos){
    // 返回子串T在主串S中第pos个字符之后的位置，若不存在，则函数值返回0
    // 其中要求：T非空，1<=pos<=StrLength(S)
    
    // 从pos位置开始查找
    // 主串从pos开始 子串从头开始
    i = pos; j = 1;
    // 从起始位置逐个匹配子串与主串的元素
    while(i <= S[0] && j <= T[0]){ // 注意，串的0下标位置存放串的长度，也即StrLength(S)
        // 逐个字符进行匹配
        if(S[i] == T[j]){
            // 若字符匹配成功，主串子串均往后走一个元素
            ++i;
            ++j;
        }else{
            // 若字符匹配不成功，主串回溯到i-j+2位置，子串回到串头重新比较（实际效果：子串整体向下一位移动）
            i = i - j + 2;
            j = 1;
        }
        // 如果找到了这么个子串（也就是j成功走到了子串的最后一个元素的后一位），那就返回这个子串在主串中的起始位置
        if(j > T[0]) return i - T[0];
        // 没找到就返回0
        else return 0;
    }
}

代码实现

#define MAXSTRLEN 255
// 定长顺序串存储表示
typedef char SString[MAXSTRLEN + 1];

int Index(SString S, SString T, int pos) {
    int n = StrLength(S);
    int m = StrLength(T);

    // 边界检查
    if (pos < 0 || pos >= n || m == 0 || m > n) {
        return 0;
    }

    int i = pos;
    int j = 0;
    while (i < n && j < m) {
        if (S[i] == T[j]) {
            ++i;
            ++j;
        } else {
            i = i - j + 1; // 从下一位置重新匹配
            j = 0;
        }
    }

    return (j == m) ? (i - m) : 0;
}

KMP算法伪代码

int Index_KMP(SString S,SString T,int pos){
    // 利用模式串T的next函数求T在主串S中第pos个字符之后位置的KMP算法
    // 其中要求：T非空，1<=pos<=StrLength(S)
    i = pos; j = 1;
    while(i <= S[0] && j <= T[0]){
        if(j == 0 || S[i] == T[j]){ // 与BF算法不同，在KMP算法中模式串回到开头(j==0)时，只能跳过当前主串字符，从主串下一个字符开始匹配
            ++i; ++j;
        }else{
            // 回退到部分匹配的位置
            j = next[j];
        }
    }
    if(j > T[0]) return i-T[0];
    else return 0;
}

emm....看上去跟BF算法基本差距主要在于next数组，那么这个数组怎么求得呢？

next数组与前后缀有关！具体定义可自行查阅资料。

void get_next(SString T,int next[]){
    // 求模式串T的next函数值并存入
    i = 1;
    // 人为定义第一个是0 ，因为模式串T的第一个字符是不存在前后缀的
    // 其实第二位也一定为1，但这里不手动定义
    next[1] = 0;
    // j 表示当前前缀长度（指向当前字符之前的最长相等前后缀的下一个位置）
    j = 0;
    while(i < T[0]){
        if(j == 0 || T[i] == T[j]){
            // 如果：
            // 1. j == 0：表示当前字符没有可以匹配的前缀
            // 2. T[i] == T[j]：表示当前字符与最长前缀的下一个字符匹配
            
            ++i;++j;
            
            // 将当前字符对应的 next 值设为 j（最长相等前后缀长度）
            next[i] = j;
        }else {
            // 如果当前字符与最长前缀的下一个字符不匹配
            j = next[j]; // 回退 j，尝试更短的前缀匹配
        }
    }
}

完整代码实现

#define MAXSTRLEN 255

typedef char SString[MAXSTRLEN + 1];

void get_next(SString T, int next[]) {
    int i = 1, j = 0;
    next[1] = 0;
    while (i < T[0]) {
        if (j == 0 || T[i] == T[j]) {
            ++i;
            ++j;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
}

int Index_KMP(SString S, SString T, int pos) {
    int next[MAXSTRLEN + 1];
    get_next(T, next);
    int i = pos, j = 1;
    while (i <= S[0] && j <= T[0]) {
        if (j == 0 || S[i] == T[j]) {
            ++i;
            ++j;
        } else {
            j = next[j];
        }
    }
    return (j > T[0]) ? (i - T[0]) : 0;
}

第五章 数组与广义表

算法5.1 稀疏矩阵的普通转置操作 O(nu * tu)

Status TransposeSMartix(TSMatrix M, TSMatrix &T){
    // 稀疏矩阵用三元组存储 求稀疏矩阵M的转置矩阵T
    // T的行数 = M的列数
    T.mu = M.nu;
    // T的列数 = M的行数
    T.nu = M.mu;
    // T的非零元个数 = M的非零元个数
    T.tu = M.tu;
    
    if(T.tu){ // 避免对空矩阵进行操作
        // 初始化指针q，指向T矩阵存储数组的起始位置，用来存储转置后的元素
         q = 1;
        // 外层循环遍历矩阵M的列
         for(col = 1;col <= M.nu;++col)
             // 内层循环遍历矩阵M的非零元素
             for(p = 1;p <= M.tu;++p){
                 // 如果当前非零元素M.data[p]的列索引（M.data[p].j）等于当前列索引col
                 if(M.data[p].j == col){
                      // 将原矩阵M的行索引（M.data[p].i）赋值给转置矩阵T的数据项的列索引
                     T.data[q].i = M.data[p].j;
                     // 将原矩阵M的列索引（M.data[p].j）赋值给转置矩阵T的数据项的行索引
                     T.data[q].j = M.data[p].i;
                     // 将原矩阵M的非零元素值（M.data[p].e）赋值给转置矩阵T的数据项
                     T.data[q].e = M.data[p].e;
                     // 移动指针q，指向下一个位置
                     ++q;
                 }
             }
     }
    return OK;
}

算法5.2 稀疏矩阵的快速转置操作 O(nu+tu)

Status FastTransposeSMatrix(TSMatrix M,TSMatrix &T){
    // 快速将稀疏矩阵M转置为T
    T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
    if (T.tu) {
    // 步骤 1：初始化并计算每列的非零元素个数
    for (col = 1; col <= M.nu; ++col) {
        num[col] = 0; 
    }
    for (t = 1; t <= M.tu; ++t) {
        // 对于每一个非零元素 M.data[t]，增加其所在列 (M.data[t].j) 的计数
        ++num[M.data[t].j];
    }

    // 步骤 2：计算每一列的第一个非零元素在 T 中的起始位置
    cpot[1] = 1; 
    // cpot 数组用于存储转置后的矩阵 T 中，按列顺序每列第一个非零元素的位置。初始化 cpot[1] 为 1，表示第一列的第一个非零元素在 T 中的位置
    for (col = 2; col <= M.nu; ++col) {
        // 通过累加每列的非零元素个数，计算出第 col 列第一个非零元素在转置矩阵 T 中的位置
        cpot[col] = cpot[col - 1] + num[col - 1];
    }

    // 步骤 3：转置
    for (p = 1; p <= M.tu; ++p) {
        // 获取当前非零元素所在列的列索引
        col = M.data[p].j;
        // 获取当前列 col 在转置矩阵 T 中的当前位置，保存在 q 中
        q = cpot[col];
        // 将 M 中当前非零元素的行列交换，存储到 T 中
        T.data[q].i = M.data[p].j;  // 将 M 中元素的列索引 (M.data[p].j) 存储为 T 中的行索引
        T.data[q].j = M.data[p].i;  // 将 M 中元素的行索引 (M.data[p].i) 存储为 T 中的列索引
        T.data[q].e = M.data[p].e;  // 将 M 中元素的值 (M.data[p].e) 存储到 T 中

        // 将 cpot[col] 递增，表示该列的下一个非零元素在 T 中的位置
        ++cpot[col];
    }  // for
}  // if
}

代码实现

#define OK 1
#define MAXSIZE 255

typedef int ElemType;
typedef int Status;

// 用三元组存储稀疏矩阵
typedef struct{
    int i, j;
    ElemType e;
}Triple;

typedef struct{
    Triple data[MAXSIZE];
    int mu, nu, tu;          //矩阵行数，列数和非0元个数
}TSMatrix;

//稀疏矩阵转置   （适用于 tu << mu × nu 的情况）
Status TransposeSMatrix(TSMatrix M,TSMatrix &T){
    T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
    if(T.tu){
        int q = 1;
        for(int col = 1; col <= M.nu; ++col){
            for(int p = 1; p <= M.tu; ++p){
                if(M.data[p].j == col){
                    T.data[q].i = M.data[p].j;
                    T.data[q].j = M.data[p].i;
                        T.data[q].e = M.data[p].e;
                    q++;
                }
            }
        }
    }
    return OK;
}

//稀疏矩阵的快速转置算法
Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
    int cpot[MAXSIZE + 1], num[MAXSIZE + 1];   //辅助数组  
    T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
    if(T.tu){
        for (col = 1; col <= M.nu; ++col) {
            num[col] = 0; 
        }
        for(int k = 1; k <= M.tu; k++) {
            num[M.data[k].j]++;
        }
        cpot[1] = 1;
        for(int col = 2; col <= M.mu; col++){
            cpot[col] = cpot[col - 1] + num[col - 1];
        }
        
        for(int p = 1; p <= M.tu; p++){
            int col = M.data[p].j; 
                int q = cpot[col];
            T.data[q].i = M.data[p].j;
            T.data[q].j = M.data[p].i;
            T.data[q].e = M.data[p].e;
            cpot[col]++;
        }
    }
    return OK;
}

第六章 树和二叉树

算法6.3 中序遍历二叉树的非递归（迭代）算法②

有两种方法 这里介绍书中的第二种

Status InOrderTraverse(BiTree T,Status(*Visit)(TElemType e)){
    // 采用二叉链表存储结构，Visit是对数据元素操作的应用函数
    // 中序遍历二叉树T的非递归算法，对每个数据元素调用函数Visit
    InitStack(S);
    // 将指针 p 初始化为树的根节点 T，p 用于遍历树
    p = T;

    // while 循环用于遍历树，直到栈为空并且 p 指针为空为止
    while (p || !StackEmpty(S)) {
    if (p) {  // 如果 p 不为空，说明当前节点存在
        // 将当前节点 p 压入栈 S，保存节点，以便后续返回到该节点
        Push(S, p);  
        // 移动到当前节点的左子树，继续向下遍历左子树
        p = p->lchild; 
    } else {  // 如果 p 为空，说明当前节点没有左子树，或者已经遍历完左子树
         // 弹出栈顶元素，将栈顶元素赋值给 p，p 指向栈顶保存的节点
        Pop(S, p); 
        if (!Visit(p->data)){
            return ERROR;
        }
        // 移动到当前节点的右子树，准备遍历右子树
        p = p->rchild; 
    }  // else
}  // while

    return OK;
}

算法6.4 先序序列创建二叉树（递归）

Status CreateBiTree(BiTree &T){
    // 按先序次序输入二叉树中结点的值（一个字符） 空格字符代表空树
    // 构造二叉链表表示的二叉树T
    scanf(&ch);
    // 如果是空字符，表示没有树的根节点，因此将树 T 设置为 NULL（空树）
    if(ch == '') T = NULL;
    else{
        // 动态分配内存给新节点 T
        if(!(T = (BiTNode*)malloc(sizeof(BiTNode)))) exit(OVERFLOW);
        T->data = ch;
        // 递归创建左右子树
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
    return OK;
}

代码实现

#define OK 1
#define ERROR 0
#define OVERFLOW -2

typedef int TElemType;
typedef int Status;

typedef struct BiTNode{
    TElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

Status InOrderTraverse(BiTree T){
    SqStack S;
    InitStack(&S);
    BiTree p = T;
    while(p || !StackEmpty(&S)){
        if(p != NULL){
            Push(&S,p);
            p = p->lchild;
        }else{
            Pop(&S,p);
            printf("%d ",p->data);
            p = p->rchild;
        }
    }
}

Status CreateBiTree(BiTree &T)
{
    char ch=getchar();
    if(ch=='.') {
        T = NULL;
    } else{
        T = (BiTree)malloc(sizeof(BiTNode));
        if(!T) exit(OVERFLOW);
        T->data = ch;
        CreateBiTree(&((*T)->lchild));
        CreateBiTree(&((*T)->rchild));
    }
    return OK;
}

第七章 图

算法7.4 7.5 深度优先搜索的存储结构和遍历

// 辅助数组，用来记录顶点是否已访问
Boolean visited[MAX];
// 用来访问函数指针
// VisitFunc是一个指向函数的指针 （int v)是这个函数的参数
// 因此这里实际上创建的是全局变量 VisitFunc
Status (*VisitFunc)(int v); 

void DFSTraverse(Graph G, Status (*Visit)(int v)) {
    // 对图G进行深度优先遍历
    // 使用全局变量，使DFS函数不需要设置函数指针参数
    VisitFunc = Visit;
    // 对整个辅助数组进行初始化为未访问
    for (v = 0; v < G.vexnum; ++v) {
        visited[v] = FALSE; 
    }
    // 对每一个顶点进行深度优先遍历
    for (v = 0; v < G.vexnum; ++v) {
        if (!visited[v]) {
            // 对未访问的顶点进行DFS操作
            DFS(G, v); 
        }
    }
}

void DFS(Graph G, int v) {
    // 从顶点v开始深度优先遍历
    visited[v] = TRUE; // 标记为已访问
    VisitFunc(v); // 执行访问操作
    for (w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)) {
        if (!visited[w]) {
            // 递归访问邻接点
            DFS(G, w); 
        }
    }
}

算法实现（邻接表存储的图）

#define MAX_VERTEX_NUM 20

typedef VertexType int;
typedef InfoType int;

// 顶点访问状态
enum VisitIf { unvisited, visited };

// 边表结点
typedef struct EBox {
    VisitIf mark;      // 访问标记
    int ivex, jvex;    // 关联的顶点
    struct EBox *ilink, *jlink; // 链接到下一个边的指针
    InfoType* info;        // 边的附加信息指针
} EBox;

// 顶点表结点
typedef struct VexBox {
    VertexType data;        // 顶点数据
    EBox* firstedge;  // 指向第一条关联边的指针
} VexBox;

// 图的定义（邻接多重表表示）
typedef struct {
    VexBox adjmulist[MAX_VERTEX_NUM]; // 顶点数组
    int vexnum, edgenum;              // 顶点数和边数
} AMLGraph;

// 辅助数组，用来记录顶点是否已访问
bool visited[MAX_VERTEX_NUM];

// 用来访问顶点的函数指针
void (*VisitFunc)(int);

// 深度优先遍历
void DFSTraverse(AMLGraph& G, void (*Visit)(int)) {
    VisitFunc = Visit; 
    for (int v = 0; v < G.vexnum; ++v) {
        visited[v] = false;
    }
    for (int v = 0; v < G.vexnum; ++v) {
        if (!visited[v]) {
            DFS(G, v);
        }
    }
}

// 从顶点v开始深度优先搜索
void DFS(AMLGraph& G, int v) {
    visited[v] = true;
    VisitFunc(v);
    EBox* p = G->adjmulist[v].firstedge; // 获取顶点v的第一条边
    while (p) { 
        w = 
        int w = (p->ivex == v) ? p->jvex : p->ivex; // 找到顶点v的邻接点
        if (!visited[w]) { 
            DFS(G, w); // 递归访问未访问的邻接点
        }
        p = (p->ivex == v) ? p->ilink : p->jlink; // 移动到下一条边
    }
}

算法7.6 广度优先遍历

void BFSTraverse(Graph G,Status (*Visit)(int v)){
    // 广度优先非递归遍历图G 辅助队列G 访问标志数组visited[]
    for(v = 0;v < G.vexnum;++v){
        visited[v] = FALSE;
    }
    // 初始化访问标志数组
    // 初始化辅助队列
    InitQueue(Q);
    for(v = 0;v < G.vexnum;++v){
        // 遍历访问未访问的结点
        if(!visited[v]){
            // 更改访问标志数组并访问顶点v
            visited[v] = TRUE;
            Visit(v);
            // 将顶点v入队
            EnQueue(Q,v);
            // 如果队列不空
            while(!QueueEmpty(Q)){
                // 队头出列并赋值给u
                DeQueue(Q,u);
                for(w = FirstAdjVex(G,u); w >= 0; w = NextAdjVex(G,u,x)){
                    // w 为 v未访问的邻接顶点
                     if(!Visited[w]){
                         Visited[w] = TRUE;
                         Visit(w);
                         EnQueue(Q,w);
                     } // if
                } // for
            } // while
        } // if
    } // for
} // BFSTraverse

算法实现 （邻接矩阵存储的图）

#define INFINITY INT_MAX
#define MAX_VERTEX_NUM 20

typedef VRType int;
typedef InfoType int;
typedef VertexType int;

typedef struct ArcCell{
    VRType adj;                      // 邻接关系（1 表示有边，0 表示无边）
    InfoType* info;
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct{
    VertexType vexs[MAX_VERTEX_NUM];
    AdjMatrix arcs;
    int vexnum,arcnum;
}MGraph;

bool visited[MAX_VERTEX_NUM];

void BFStraverse(MGraph G){
    for (int v = 0; v < G.vexnum; v++) visited[v] = False;
    SqQueue Q;
    InitQueue(&Q);
    for (int v = 0; v < G.vexnum; v++)    {
        if (!visited[v]){
            visited[v] = True;    Visit(v);
            EnQueue(&Q, v);
            while (QueueEmpty(Q)){
                int u;
                DeQueue(&Q, &u);
                for (int w = 0; w < G.numVertexes; w++){
                    if (G.arc[u][w] == 1 && !visited[w]){
                        visited[w] = True;
                        Visit[w];
                        EnQueue(&Q, w);    
                    }
                }
            }
        }
    }
}

第九章 查找

算法9.2 折半查找（二分查找）

// very Easy
int Search_Bin (SSTable ST,KeyType key){
    // 在有序表ST中查找关键字为key的元素
    // 找到返回对应位置，否则return 0
    low = 1 ; // 左
    high = ST.length; // 右
    while(low <= high){ // 左右相遇终止
        mid = (low + high) / 2; // 相当于逻辑右移一位（速度快点）
        if (EQ(key,St.elem[mid].key)) return mid; // 找到了
        else if (LT(key,St.elem[mid].key)) high = mid - 1; // key比当前的要小，移动high
        else low = mid + 1; // key比当前的要大，移动low
    }
    return 0;
}

算法实现 C

typedef ElemType int;

typedef struct{
    ElemType* elem;
    int length;
}SSTable;

int Search_Bin (SSTable ST,int key){
    int left = 1;
    int right = ST.length - 1;
    while(low <= high && mid = (left+right) >> 1){
        if(St.elem[mid] == key) return mid;
        else if (St.elem[mid] > key) right = mid - 1;
        else left = mid + 1;
    }
    return 0;
}